曲线元素

在之前的博客文章中，我们讨论了有限元法 (FEM) 用于模拟曲面光学结构的独特功能。在 2D 中使用三角形网格和在 3D 中使用四面体网格的能力允许线性近似弯曲边缘。这种近似的质量和精度可以通过减小沿弯曲边缘的网格大小来提高。另一种方法是使用本身具有弯曲边缘的元素，即所谓的曲线或等参元素

这篇文章将概述曲线元素。我们将涵盖：

曲线元素可以帮助解决的基本问题

数学基础曲线元素。

量化曲线元素的影响。

简述曲线元素

线性元件

例如，让我们看看对半径为 1 的圆的右上象限进行网格划分的不同方法。

在这种情况下，圆边缘元素的边长约束已设

置为 1，等于圆的半径。这是一个粗网格约束，圆的曲线近似不好。

我们现在将圆边缘元素的边长约束更改为

0.1，即圆半径的十分之一。这是一个更精细的网格约束，曲线边界的近似变得更准确。这是以沿圆边缘的元素数量增加为代价的。

曲线元素

继续我们的示例，我们可以指定圆形象限应使用曲线元素，而不是在边界处使网格更细。

在这种情况下，圆边缘元素的边长约束已设

置为 1，与我们的第一个示例相同。在这里，我们为属于圆的元素指定了 2 的曲线度。这样做时，扇形的外部边界边缘变得弯曲。这允许用很少的元素很好地近似圆边界。

曲线元素的数学

在这一部分中，我们将简要介绍使用曲线元素的数学基础。为了更完整的讨论，我们参考以下文献：

I. Ergatoudis, BM Irons, OC Zienkiewicz,用于有限元分析的弯曲、等参、“四边形”单元，《国际固体与结构杂志》，4(1)，第 31-42 页，(1968)

M. Plock，在曲线元素上使用不连续伽辽金时域方法对等离子体纳米结构进行数值分析，硕士论文，柏林洪堡大学，（2020 年） 此外，本节中显示的数字经 M. Plock 的论文许可复制。由于我们在帖子中一直在研究三角形网格，因此我们将继续考虑三角形网格元素。同样的考虑也适用于其他单元类型，如四边形、四面体、棱柱形等。

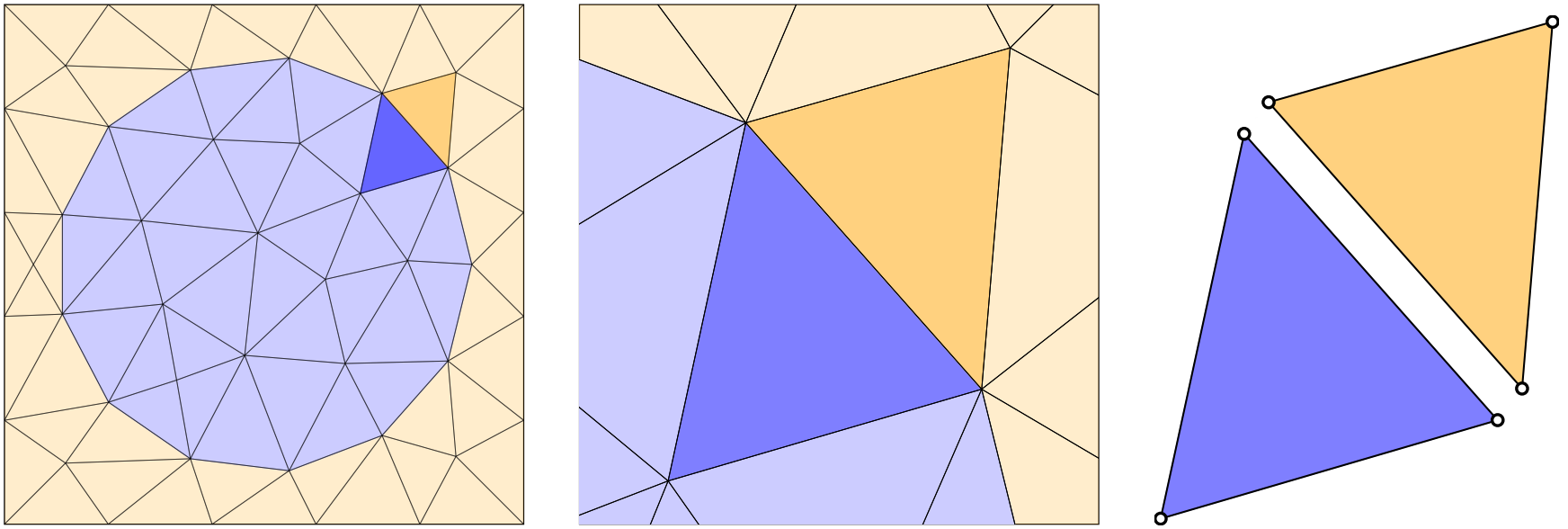
球形几何通过线性元素粗略地近似。关注三角形边缘元素之一，我们可以孤立地考虑这两个元素及其关联节点（白色圆圈）。

考虑形成上述网格中圆形对象边缘的三角形元素。取一对具有公共边界的蓝色（内部）和橙色（外部）三角形网格元素，可以看出这两个元素中的每一个都完全通过它们的三个角节点来描述。这是因为节点之间的边界是直线（即线性），我们只需要一个起点和终点来描述这些边中的每一个。

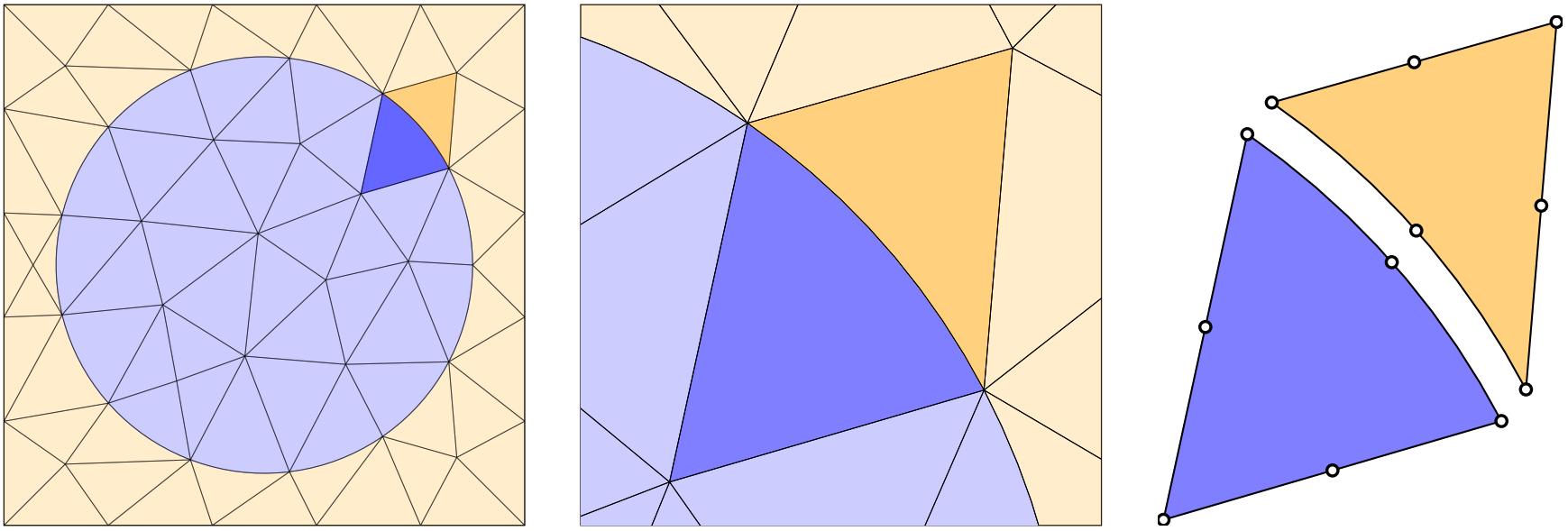
通过曲线元素可以更好地近似球形几何形状。关注相同的两个三角形边缘元素之一，我们认识到它们现在共享一个弯曲的边界。当我们还绘制它们的关联节点（白色圆圈）时，弯曲边界的原点变得更加清晰。通过在每个三角形边元素的中心也有节点，它允许边在这种情况下描述一条二阶多项式曲线。

我们现在转到上面网格中圆形对象中显示的具有弯曲边缘的三角形元素的示例。再次，取一对具有公共边界的蓝色（内部）和橙色（外部）三角形网格元素，可以看出这两个元素中的每一个都完全通过它们的三个角节点和边界上的一个边缘节点来描述。这是因为曲线边界是一个二阶（即二次）多项式，需要至少三个独立点来描述。其他两条直边也使用每条边三个节点来描绘，即使这些边是线性的。这是因为我们需要三角形沿每条边具有相同数量的节点（更多内容见下文），但当然，也可以使用三个或更多点来描述线性边。 通过增加三角形元素的边缘节点的数量并使用更高阶的多项式，可以进一步采用这一基本思想。事实上，我们可以概括网格节点的总数N 给定多项式阶的三角网格所需 米 作为：

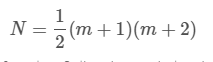
以前的博客文章已经涵盖了参考元素的概念。在执行有限元模拟时，麦克斯韦方程通常在参考元素上求解，然后映射到模拟中使用的真实物理元素上。参考元素通常在单位区间上，

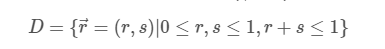
该映射至少需要沿三角形外部保存节点的数量和相对顺序。此外，我们需要来自参考元素的映射D 到物理元素 D克：

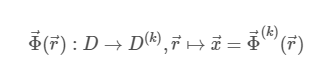
一般来说，这个映射函数是一个多项式 r 回答 秒 ：和 米 是映射的顺序和 一种~我Ĵ 是向量值展开系数。为了 米= 1 我们保留标准线性元素 米≥ 2 给出更高阶的网格。

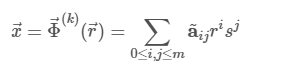
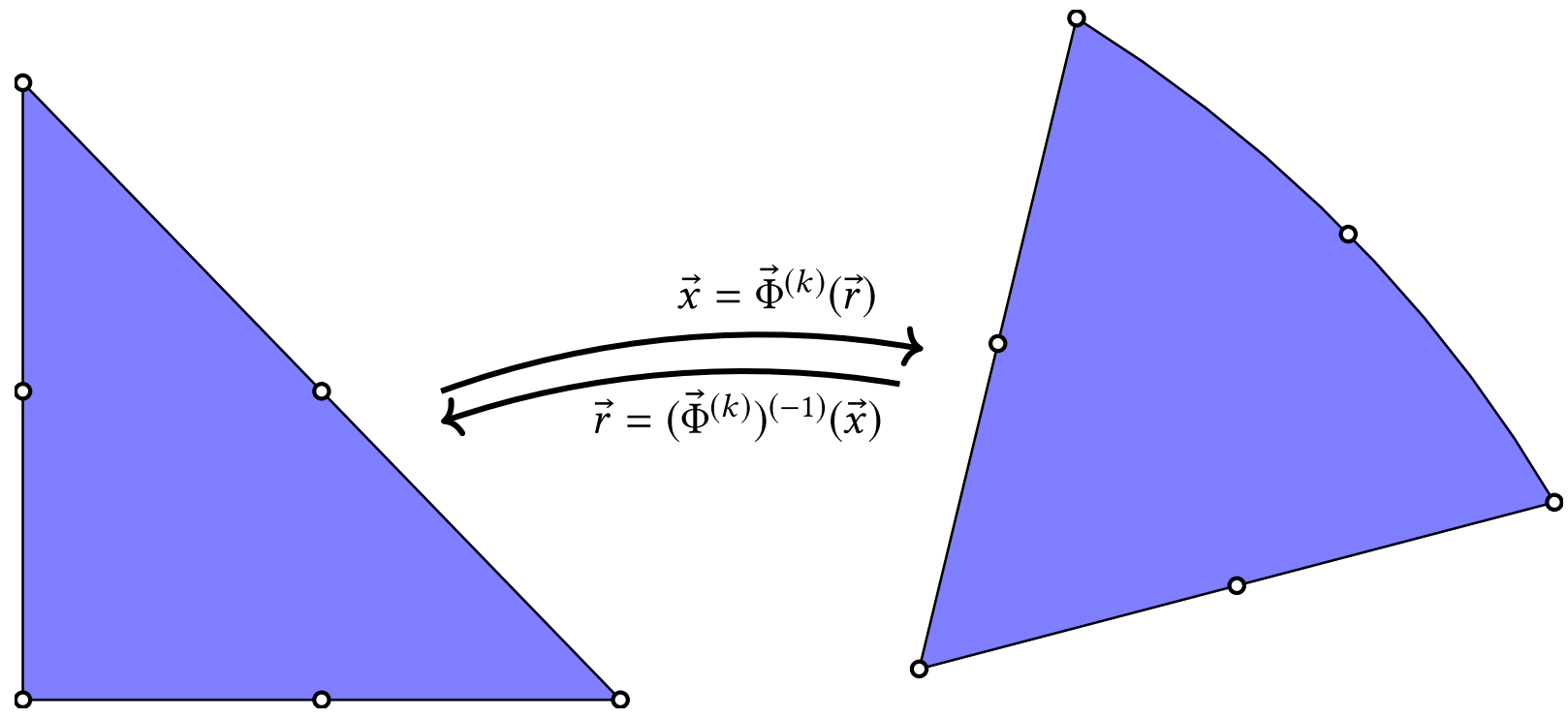
使用曲线元素，我们需要能够计算从参考三角形到具有弯曲边缘的三角形的变换。请注意，两个三角形具有相同数量的角节点和边节点。 为了使变换函数的概念更具体一些，我们展示了线性的一般形式的例子，

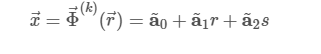
和二阶，

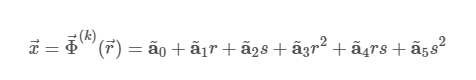
变换函数。为了完成对曲线元素的描述，我们需要计算实际系数 一种~ . 为此，我们首先定义一个向量 r⃗ n= (rn,秒n) ，它描述了 n - 参考元素上的第 -th 个节点。现在我们构造一个 N× N 我们将称之为矩阵 伏 ，Vandermonde 矩阵，使用位置向量：

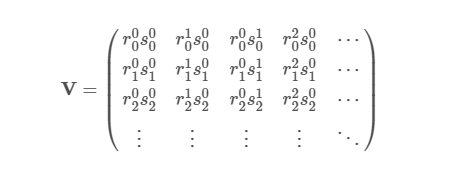
有了这个矩阵，我们继续定义另外两个向量。首先，由网格节点在物理元素上的位置构成的向量D克,

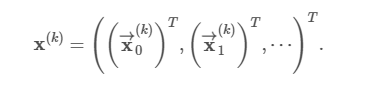
后面跟着一个由未知膨胀系数组成的向量，

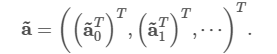
由于建设 伏 它认为，

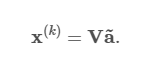
由于范德蒙矩阵的可逆性，我们可以通过对矩阵求逆来获得未知的展开系数 伏 ,

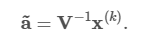
通过这最后一步，映射 Φ⃗ （ķ ）(r→) 和逆映射 (Φ⃗ （ķ ）)− 1(X→) 完全指定。

曲线元素的收敛

我们已经介绍了曲线元素的基本概念及其数学基础，现在是时候看看数字了：曲线元素可以为我们做什么？

为了检验曲线元素的优势，我们研究了来自具有圆形横截面的无限圆柱体的光散射。圆柱体具有与银相同的介电常数，周围的材料是空气。入射光的波长为 347 nm，圆形截面的半径为 50 nm。已选择这些参数使得存在等离子体共振（对于平面偏振光）。

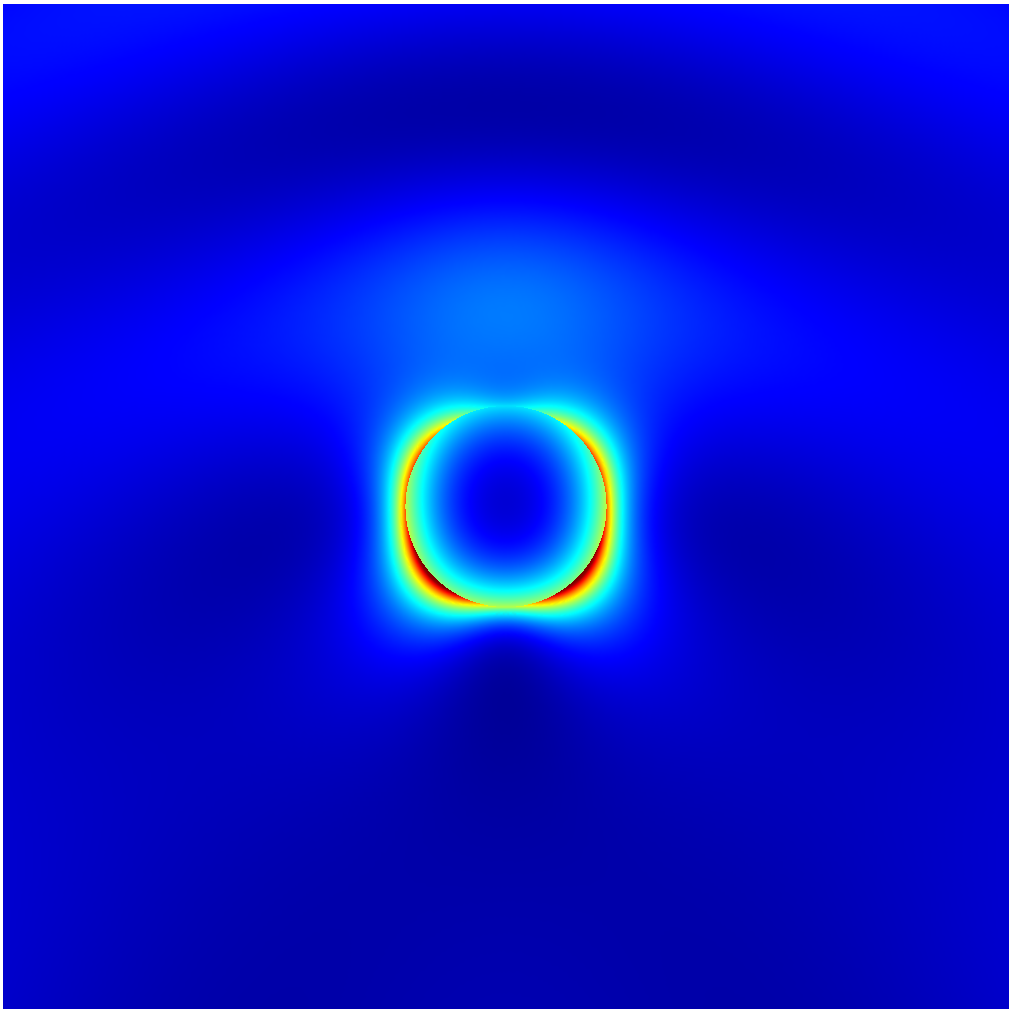
电场强度强烈地集中在圆形散射体的表面。

因此，我们的目标是平衡两个误差源，即几何描述中的误差和电场解描述中的误差。

为了比较不同场解的精度，我们比较了归一化的散射截面 问小号Ç一 无限圆柱体，也可以解析计算。我们比较了四种不同的细化策略，以减少我们的数值确定的值的相对误差 问小号Ç一 与分析值相比。为了比较不同的策略，我们将所有策略绘制为用于求解系统矩阵的数值未知数的函数。更多的未知数意味着需要更多的时间来完成模拟和需要更多的内存。目标是选择数值设置以获得可接受的最小误差的最小数量的未知数。误差的收敛和使用的四个网格如下图所示。

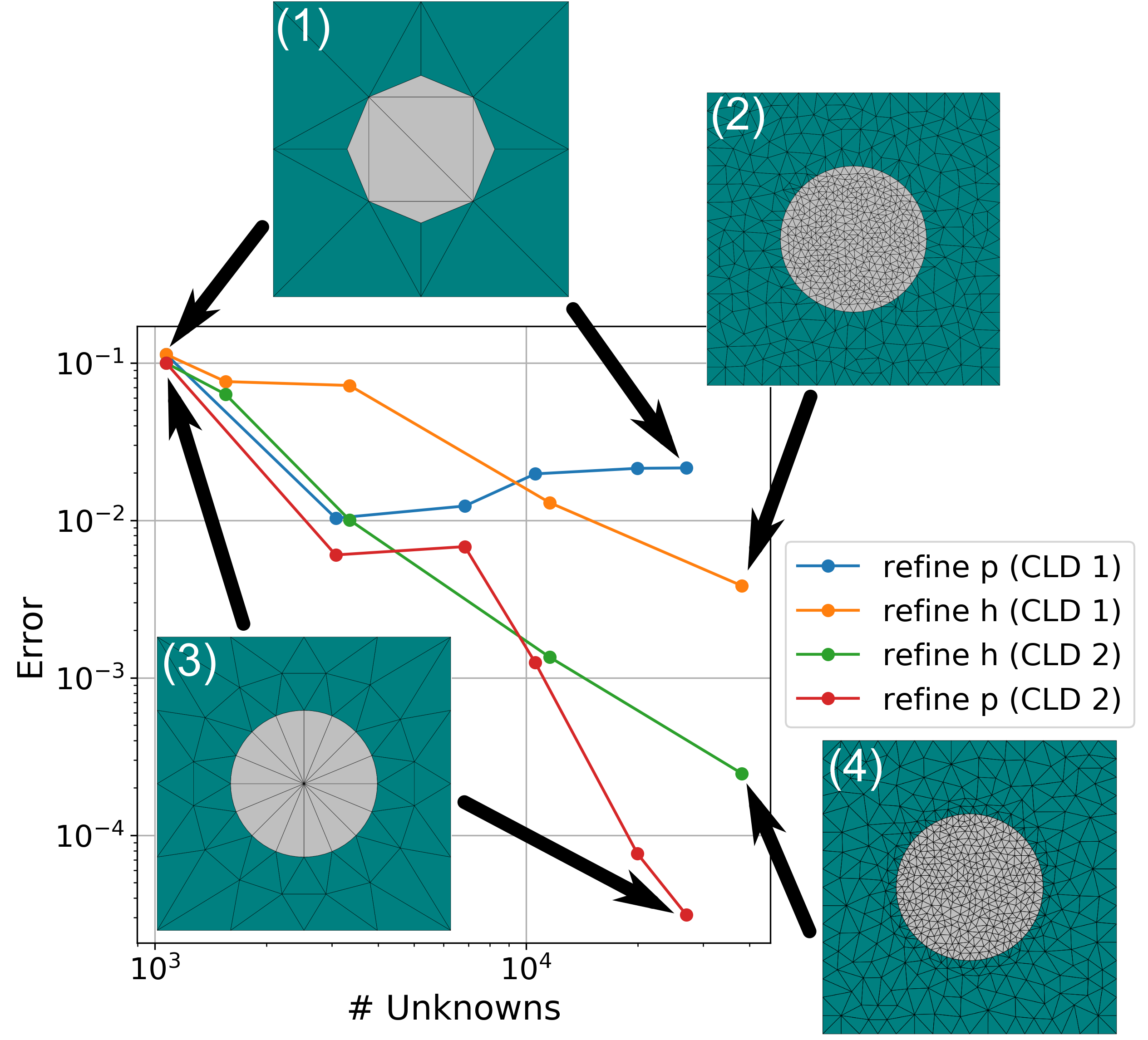
四种不同的改进策略，用于减少来自圆柱形等离子体散射体的散射的相对误差。图中指示了用于与某些点相关的模拟的网格。

作为我们的起点，我们使用粗网格描述几何形状，并使用低有限元次数来逼近电场。课程网格 (1) 显示在图像的左上角。圆形横截面的近似值仅使用六个三角形，这意味着我们获得了具有直边和尖角的东西。圆形横截面的曲线度 (CLD) 已设置为 1，表示线性元素。

增加有限元度 磷 在整个网格中（细化 磷 使用 (CLD 1))，误差（蓝色曲线）减少为 磷 增加，但最终饱和 2 ⋅10− 2 . 我们无法进一步减少错误 磷 细化，因为几何误差占主导地位。

减少网格长度 H 在整个网格中（细化 H with (CLD 1)) 导致网格显示在右上角 (2)。误差（黄色曲线）减少为 H 下降，但速度比 磷 收敛。然而，误差不断减小，达到大约 5 ⋅10− 3 . 我们能够低于先前模拟策略的误差，因为更精细的网格具有更低的几何误差。尽管如此，误差会随着使用的未知数的增加而缓慢降低。

提出的第三个策略是网格长度 H 细化结合曲线度 (CLD) 为 2（绿色曲线）。CLD 2 的粗网格显示在左下角 (3)，而 CLD 2 的细网格显示在右下角 (4)。包含很少元素的粗网格能够解析散射体的圆形边缘。最初，较高的曲线度不会显着减少误差。请记住，由于网眼长度较高 H 和低有限元度 磷 ，求解误差也很大。一旦 H 细化开始时，使用 CLD 1 和 2 的网格细化之间大约有一个数量级的差异（比较黄色和绿色曲线）。收敛速度（曲线的梯度）近似相等，曲线度越高，误差越小。这允许使用相同数量的未知数获得更准确的解决方案。

提出的第四个也是最后一个策略是增加有限元度 磷 CLD 为 2（红色曲线）。(3) 中显示的网格用于所有模拟。该策略为最少的未知量提供了最低的误差。这与有限元理论一致，该理论假定在某个几何误差以下， 磷 改进比 H 减少求解误差的改进。曲线度数允许我们使用较少的网格元素来降低几何误差，从而提高效率 磷 细化用于较粗的网格。

总结本节：

磷 由于几何误差占主导地位，对过于粗糙的网格的细化会以高误差饱和。

H 细化和有限元次数 1 减少了求解误差和几何误差，但该策略不是非常有效

H 细化和有限元阶数 1 显示曲线阶数 1 和 2 的收敛速度相似。

曲线度 2 提供了持续减少的误差 H 与曲线阶数 1 相比的改进。

磷 对曲线度为 2 的粗网格进行细化是本研究中最有效的细化策略。这 磷 细化减少了求解误差，而曲线元素减少了几何误差。

结论

在这篇文章中，我们介绍了曲线元素的概念，研究了该方法的数学基础，并展示了一个实际示例，展示了曲线元素的威力。与纳米光学模拟中的许多概念一样，是否使用曲线元素的决定取决于手头的给定问题。通常曲线元素在以下情况下会很有用，

几何体的一部分是弯曲的。

网格比较粗。

由于（1）和（2）引入的几何误差大到足以限制模拟的准确性。