贝叶斯最不方形重建

这是一系列专门讨论参数重建的第三篇博文。有关基本概念的介绍

在这篇文章中，我们将应用一个非常有效的方法来查找参数值$p=1，+点，p_M美元，最适合一组测量$y=*1，+点，y*_K$。与前一篇文章一样，物理测量过程由兽医函数（开始[方程] [数学]： [数学[p] 在 [数学 [x] 子集 ] 数学 [r]m [ 地图] 数学 [y] 在数学 [r] k 中 [结束[方程]，它绘制了$M的维度参数矢量[mathbf]0$到一个$K美元的输出矢量[mathbf]y]$，可以用一些假定的高斯添加噪声与方差[varepsilon_1]2，[点，]varepsilon_K=2美元。

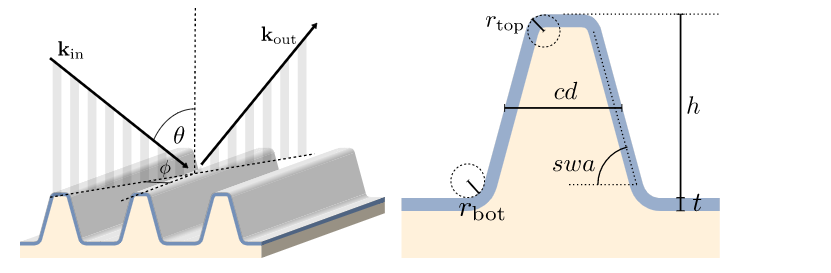
作为一个具体的例子，我们再次考虑在第一篇博文中引入的散射测量设置。单色极化紫外光，波长为266美元，以特定角度击中周期性的拉梅拉光栅。"\theta，\phi$"。光线从亚波长光栅反射，强度通过实验测量。光栅由向量 [数学[p] [cd，h，swa，t，r_]，r_\rm 机器人]\T$与六个条目（见下图）进行参数化。

在首篇文章中，我们还介绍了点估计 [数学][rm ML]$的最有可能的模型参数给定量测量媒介 $[数学]\$： [开始] [数学][[rm ML] [ 下集 [ 数学 [p] [\\m arg]， min] [数学][p]] [文本][chi]2 [数学]） [ sum_ [i]1] k ] 左 [frac]_i ] f_i [数学]] [varepsilon_i] ]右] [结束] 等式]

作者简介

Eric C.Fest是美国雷神公司资深光学设计工程师，擅长偏振光学、光度学、传感器设计、地球测量等。

如何解决最小化问题

将功能最小化的问题可以通过几种方法加以解决。在许多工程领域，对完整测量过程进行模型的函数非常昂贵。因此，最小化算法应尽可能少地使用函数评估。以我们深思熟虑的例子为例，对"数学"的评价需要解决麦克斯韦的方程问题，即确定事故光在纳米结构上的散射过程，从多个角度计算。根据计算机硬件和并行程度，计算可能需要从几秒钟到一分钟以上，每个参数集 $mathbf\p=$。

在之前的一篇博文中，我们讨论了几个不同的优化算法的应用领域 - 下坡简单，L-BFGS-B，微分演化和贝叶斯优化。由于我们通常有一个中等数字$M<30美元的参数重建和前进模型需要模拟时间通常超过5秒，Bayesian优化是最好的合适的方法，以尽量减少 $+chi 2 （+mathbf[p]）$。贝叶斯优化使用统计推理（高斯过程回归）根据以前对目标函数的所有观测来预测看不见参数的函数值。有关介绍，请参阅关于高斯工艺回归和贝叶斯优化的博客文章。

然而，由于我们正在处理一种特殊的最小化问题，即非线性最小方形问题，因此存在更专业的算法，如高斯-牛顿算法和莱文伯格-马夸特算法。他们两人都利用了基础二次结构，即"数学"[数学][p]$。为了确定下一个取样点，希望价值更小，为 $chi=2 （+数学\p]），他们将模型功能扩展到本地，直线顺序。这两种方法的收敛都相当不错。然而，它们有两个限制：（1） 它们可以收敛到非最佳的本地最低值，而错过全球最低值。（2） 局部线性近似限制了方法的准确性和效率。

在以下方法中，我们考虑了另一种方法，贝叶斯最小方形优化，它结合了贝叶斯优化（准确的统计推论、快速的全球趋同）和高斯-牛顿和莱文伯格-马夸特方法（利用基础二次结构[chi]2[数学]）]）的优势。

该方法的想法是使用$K $高斯流程 $[rm GP]1，[点]，[rm GP]_K美元，这些流程经过了以前对通道功能的评估$f_1（数学[p]），[点]，f_K（[数学]）]）$。根据高斯流程预测，确定下一个采样点，以极高的概率将 $2（数学+p=）降至最低（见下图）。该方法基于A.K.乌伦霍尔特和B.S.詹森PMLR 2661（2019）引入的方法。Plock等人讨论了纳米计量方法的应用细节。亲间谍11783 （2021）.

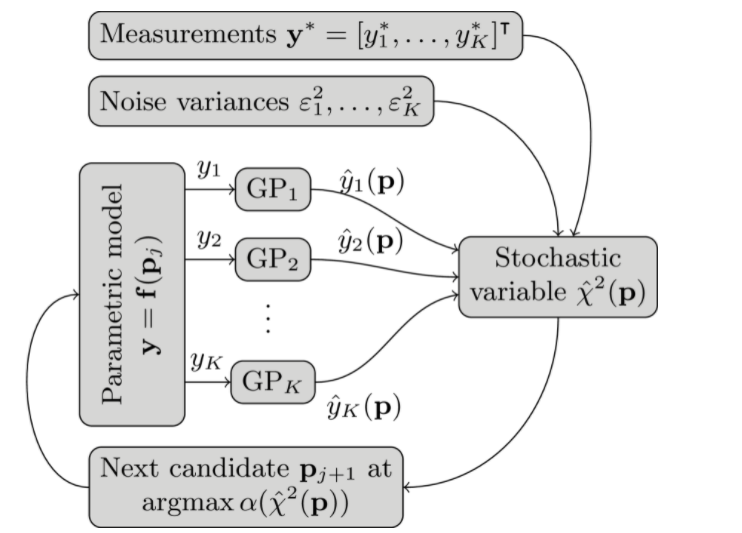
贝叶斯最不方优化的理念：

1、高斯处理 [rm GP]1，[点，\rm GP]_K$接受培训，每个通道的功能值为 $1，+点，K$，以及每个先前评估的参数矢量 $[mathbf]p=1，[点]，数学[p]_j$。

2、对于任何参数向量 $mathbf[p]$，高斯过程以$K $高斯随机变量 [帽子y_1]），[点]，帽子y_K（[数学]）$（按平均值和方差指定）的形式进行预测。

3、根据测量 $mathbf [y]和测量噪声差 [varepsilon_1]，[点varepsilon_K]2 美元的值 [chi][数学][p]]$可以以遵循非中央奇方分布的随机变量的形式进行预测。

4、基于此分布，确定下一个参数向量 [数学]j=1=$，最大限度地提高一些获取功能 $α （#hat_chi=2）$（例如，较低的置信度），因此，以高概率最大限度地降低 $2 [数学]p]） $。

散射测量示例

在以下几项中，我们尝试根据在德国国家计量研究所 PTB 获得的一组测量结果重建上述线路光栅的参数。M. Wurm等人报告了测量配置的细节。米亚斯。 技术技术 22， 094024 （2011）.测量集包含 42 美元/5° 和 87° 之间的强度，即 5+ 和 0+ circ=90$0。两套都是S和P两极分化获得的。

相应的模型功能在此 Jupyter 笔记本附带的巨蛇包中实现。该包还包含实验数据和运行分散过程 FEM 模拟的功能。ForwardProblem

下面的图显示了测量的分散强度，包括其估计的测量误差（彩色误差条），以及通过使用 JCMsuite 对散射过程进行数值模拟来预测强度，$cd= 25=，\rm nm]$， $h = 50 美元， [rm nm] $， $swa = 90 ] 0 =$t 3]， [rm nm] $， $r [rm 顶部] = 10]， [rm] $， 和$r [\rm 机器人] = 10]， [rm nm] $（行） 。

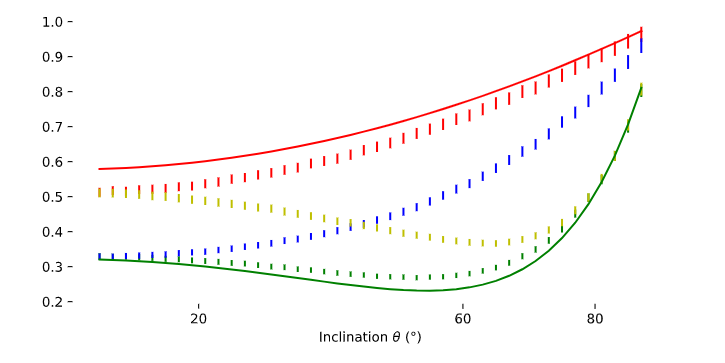
正如我们所看到的，所选参数值可能不正确，因为模型值远远超出了测量结果的不确定性间隔。只有P极化和"phi+0+circ"的测量结果才合理地同意该模型。然而，在之前的博客文章中，我们看到这些测量几乎不包含任何有关参数值的信息。

最大可能性参数值

因此，让我们找到设置的最大可能性参数（即最低 $=2$）。首先，我们创建一个客户端对象，以便与分析和优化工具包进行通信，该工具包在后台自动启动。

我们定义参数的搜索域。对于以后的使用，我们还会指定 LaTeX 格式的参数名称列表。

并非适用于域中的所有参数组合，定义了有效的几何形状。例如，氧化物层$t$的厚度不能大于顶部半径$r[\rm 顶部]$，它本身不能大于结构顶部宽度的一半 [frac{1}{2}]左（cd= [c]\n[swa]]]右）$。总共必须履行四个限制，如果约束得到履行，则由负函数定义。

受约束的搜索域可被视为一个平面的优先分布，即我们假设在受约束的域内查找参数值的概率是恒定的，外部是零。

有了有关域和约束的信息，可以创建贝叶斯莱斯广场驱动程序的新对象。Study

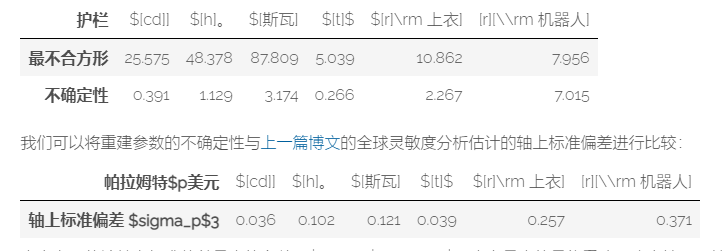
我们可以通过调用study.set_parameters（）来配置研究。对于最小夸大优化，我们需要指定测量的目标向量和测量不确定性的载体。此外，我们定义优化预算。max_iter=50

模型功能本身在带有此 Jupyter 笔记本的巨蛇包中实现。例如，它包含实验数据和运行分散过程 FEM 模拟的功能。ForwardProblem

使用该包，我们可以定义返回观测对象的研究的客观功能，其中列出反射光的所有强度，即列表 $f_1 [数学]），[点]，f_k（[mathbf[p]]]$。

现在，我们可以运行实际最小方形。

研究完成后，我们可以通过拨打study.info（）[min_params]来检索参数，并找到最少的 =chi=2$值。让我们看看最小方参数值是否导致模型函数值与测量结果一致。

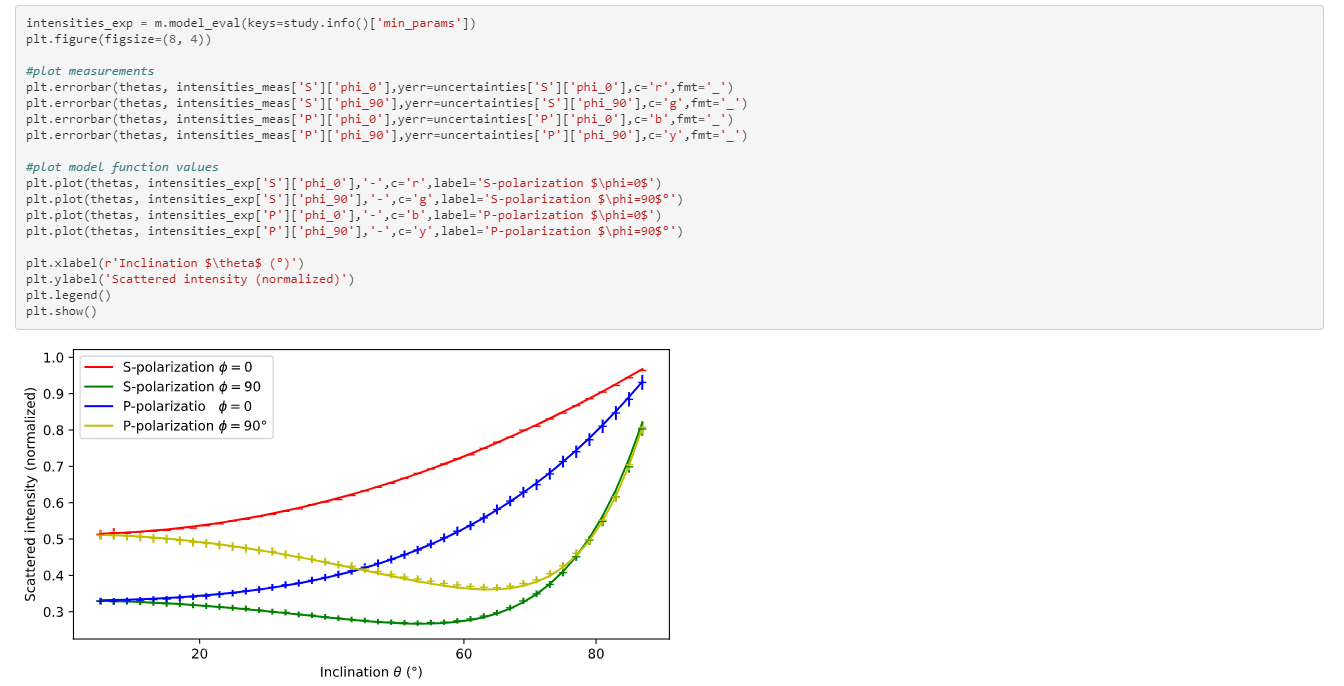
显然，对最小方形参数值的模型预测非常适合测量不确定性中的测量。

信心界限

除了重建参数的价值外，了解它们的置信间隔通常很重要。在这个系列的第一篇博文中， 我们得出参数值的不确定性大约是作为 $sigma_ [p_i] [平方米] [cot] 数学 [cov]， $$， 其中 [rm MSE] [frac] [2] [rm 分钟] [K - m] $是平均方形错误 （即. 每个自由度度的方形错误） 和 [数学 [Cov] [左 [数学] [顶部] [数学] [数学] 右] [- 1] $是参数共差矩阵与雅各比矩阵 [数学 J] $和重量矩阵 [数学[W] [[rm 诊断] 左 [[varepsilon_1]， [cots]， [varepsilon_K] [右] $ 。[rm MSE]$值和共差矩阵 [数学]可以通过拨打study.driver_info获得 。

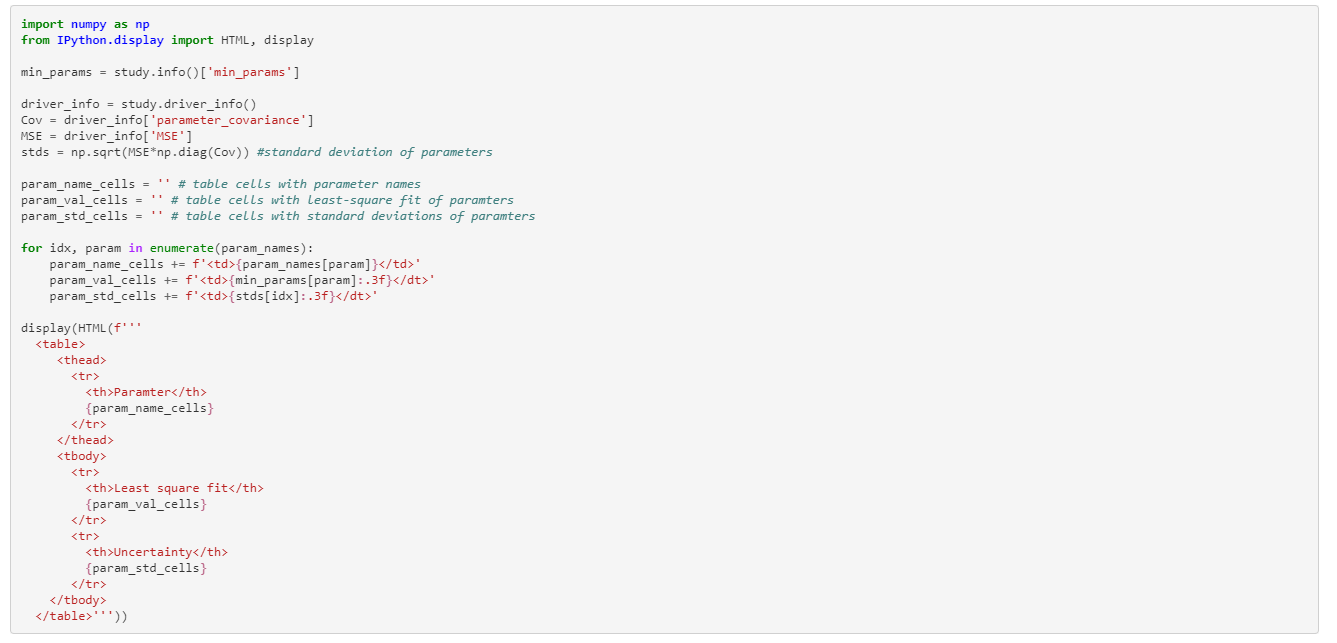
事实上，估计轴上标准偏差最大的参数，$r[rm]和$r\rm bot]$，也有最大的最终重建不确定性，而轴上标准偏差最小的值，$cd美元和$t美元，可以在最小的不确定性下重建。这再次证明，全球灵敏度分析可以为实验设置重建某些参数的能力提供重要的见解。

参数值的后分布

到目前为止，我们已经研究了参数值的最大可能性点估计值 [开始] [数学][[rm ML] [下集] [数学][ p] [rm arg]， min] [chi][[数学 [数学][文本];[奇][数学][[数学]左[frac]]_i - f_i[数学]][varepsilon_i]]右]]结束 [方程] 和在信任区间取决于共差矩阵 [数学 [Cov] [左] [数学][顶部] 数学 [数学] [右] [-1] 基于前方模型的线性近似值 [开始 [方程] [数学][数学][f] 数学 [rm Ml]] [数学 [j] [数学][ 数学 [p] [ 数学 [rm Ml]] [文本][数学[J]][j]][左]部分f_i[数学[p][部分p_j]右|[数学][数学][数学][p][rm ML]][结束[方程]

现在，我们更进一步：

1、我们希望考虑模型对参数值的非线性依赖性。为此，我们使用所有测量通道中训练有素的高斯工艺。

2、我们希望考虑有关参数的先前信息。到目前为止，我们假设所有参数值在受约束的搜索域内具有相同的先前概率。现在，假设我们知道线性光栅的参数遵循正常分布，具有$cd = （25 = pm 5）[rm]，h=（50~pm5）\rm=nm]， swa = 87 = 环 [ pm 1]， t = （4.5] pm 1）[rm nm]， r_ [rm 顶部] [10]pm 3] [rm nm]， r_ [rm 机器人] = [8 pm 3]\ rm = nm= $。

3、通常，测量错误并不完全清楚。因此，我们希望用更灵活的误差模型来替换固定的测量方差 $varepsilon_1=2，\cdot varepsilon_K s，[2]，用于测量方差 $varepsilon_1 =右栏=eta_i=2[数学]，a，b] 10 [a] f_i [数学[p]] 大] 2 = 大 [10]=b] $2.$错误模型参数应统一分配$1 =leq a =leq 3 $和 $2=leq b= leq 4$。

根据第一篇博文，鉴于模型和错误参数的概率$p（数学，a，b）$， 鉴于测量结果，参数值的后概率分布为 $p =数学[b]，a，b | [数学]] [数学]， a， b） [prod_ [i]1]k]frac{1} [p][ 2] eta_i [数学]，a，b） [左] - 弗拉克{1}{2}] 左 [frac][_i] - f_i [数学]] eta_i [数学]， a， b] [右] 2] 右] 。$$

可以使用马尔科夫链蒙特卡洛（MCMC）采样从这个概率分布中提取样本。一旦提供了大量的样品从后，人们可以确定分布的特征数字。例如，人们通常指出下 16% 的量度、50%（即中位数）和参数值的上 84% 量。

在将 $2=2 美元降至最低期间，我们已经对高斯流程进行了培训。为了进一步改进高斯过程预测，我们绘制了更多接近最大可能性点估计的样本。使用BayesLeastSquare驱动程序的关键字，可以在高斯工艺预测仍具有重大不确定性的位置绘制样本。让我们再抽50个样本（即总共100个样本）。explore_max_likelihood

现在，我们使用驱动程序参数分别定义了高斯之前的参数分布、错误模型和错误模型参数的分布。distributionerror_modelerror_model_parameter_distribution

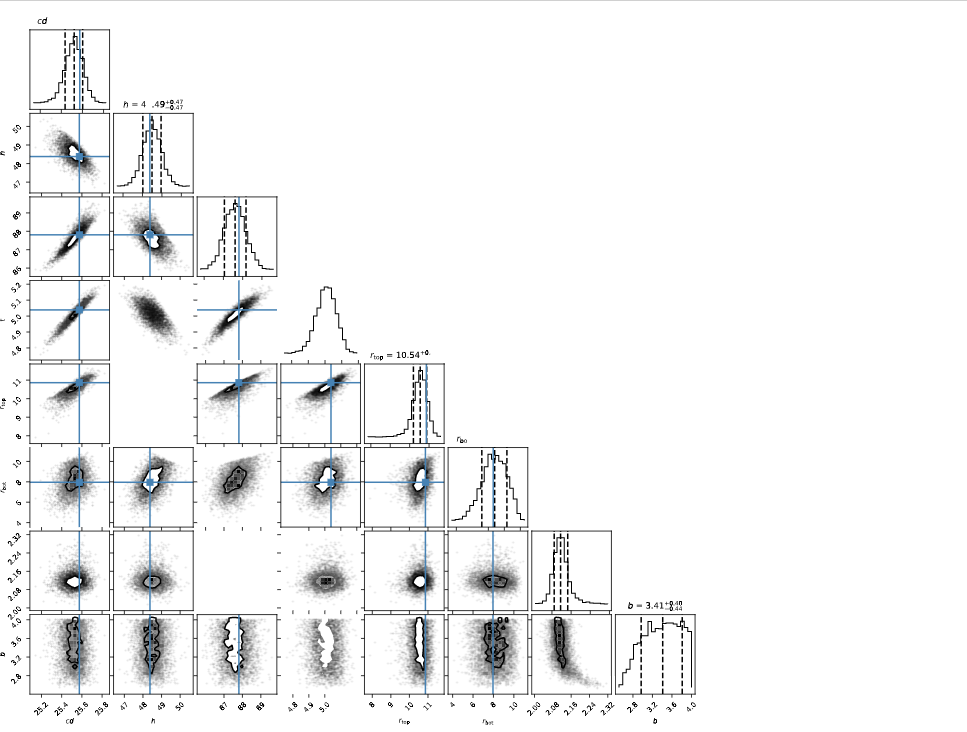
我们使用 32 个步行者运行 MCMC 采样，每个步行者运行 10，000 次迭代。从高斯工艺中抽取 320，000 个样本可能需要 30 多分钟。然而，与使用原始前向模型绘制相同数量的样本的时间相比，这次几乎可以忽略不计的时间。在内部，分析和优化工具包使用巨蛇包运行 MCMC 采样，这也提供了良好的教程，并简要介绍了 MCMC 采样的理论背景。emcee

绘制的 32 万份样本中有许多必须忽略。在初始采样阶段（"燃烧"阶段），参数尚未根据概率分布分布。此外，每个步行者的连续样本具有很强的相关性，因此彼此之间并不独立。通过绘制样本的返回子集，我们可以生成一个角图，显示通过高维后概率分布的切口。蓝色标记表示最大可能性点估计值。该图还包括每个参数（破折号线）的 16%、50% 和 84% 的量度。

结论

参数重建主要概念的介绍：我们得出了参数的概率分布、最大概率点估计值及其信心间隔，这些参数由其近似高斯概率分布的标准偏差定义。 使用 JCMsuite 对间接测量设置进行基于差异的灵敏度分析：目标是查看哪些测量对某些样本参数的值敏感，从而包含相关信息，以便从测量中重建这些值。 在上一篇博文中，我们看到了如何使用 JCMsuite 来查找最大可能性参数及其高斯式置信区间，以解决典型的散射测量问题。我们还讨论了使用高斯过程回归和 MCMC 采样获得重建参数完整后分布的更普遍案例。