导语

Paritosh 是 Wolfram 的核心开发人员，利用业余时间使用 Mathematica 来研究并模拟流体动力学问题，开发了WindTunnel2DLBM 程序包(https://blog.wolfram.com/data/uploads/2019/10/WindTunnel2DLBM.zip) 。LBM 与 IBM 的结合使用，对研究和分析流体流动是一个很好的工具。借助 Mathematica 的内置函数，实现数字风洞的组装变得非常简单。

我在学生时代学习流体动力学时，学的都是复杂的方程式以及各种简化和处理这些方程式的方法，以获得某个结果。遗憾的是，当要获得流体在不同情况下如何流动的直观感受时，这让想象力几乎没有什么空间发挥。当我上完第一节实验流体动力学课后，我了解了如何使用不同的可视化技术来定性地了解流体行为。这些可视化方式提供了一种创造性地查看流体的方法，并且，效果令人惊艳。所有这些实验和可视化都在风洞 (wind tunnel) 内进行的。

创建我们的计算型风洞

风洞是实验流体力学研究人员用来研究物体在空气（或任何其他流体）中移动时所产生的影响的设备。由于物体本身无法在管道内移动，因此通常采用高速风扇提供可控气流，而将物体放置在气流路径中，从而产生与物体在静止空气中移动相同的效果。这种实验对于理解物体的空气动力学非常有用。

风洞有不同的类型。最简单的风洞是空心管或方盒，该风洞的一端装有风扇，另一端是敞开的，这种风洞称为开放式回风风洞。从实验上讲，这种风洞不是最有效或最可靠的，却很适合构建一个计算型风洞（这正是我们这篇博文要实现的目标）。这是我们要开发的风洞的基本示意图：

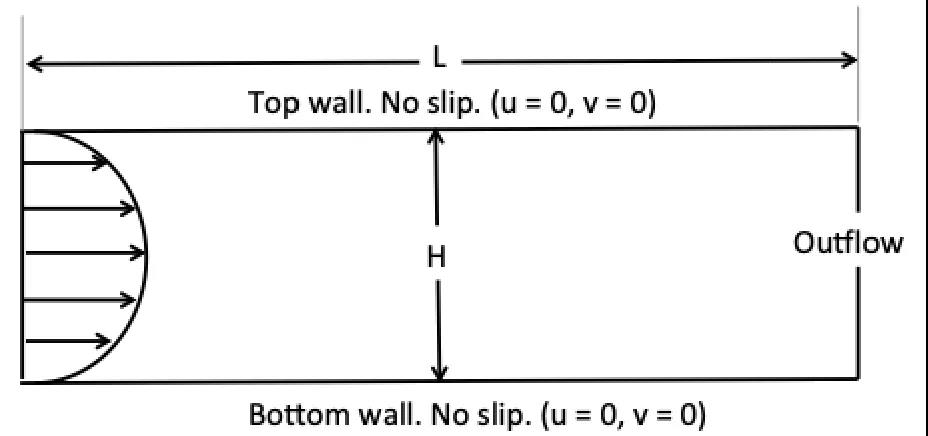
我们的风洞是一个二维风洞，流体从左侧进入，然后从右侧流出，顶部和底部是坚固的墙壁。应该指出，由于这是一个计算风洞，我们在选择边界类型上有很大的灵活性。例如，我们可让左壁、右壁和底壁固定，而顶壁可以移动，这样我们就拥有了一个很常见的风洞类型。

当人们思考计算流体力学时，总会立刻想到著名的纳维-斯托克斯方程。这组方程是决定流体流动行为的控制方程。在这一点上，我们似乎要使用纳维-斯托克斯方程来帮助我们建造一个风洞。但事实证明，还有其他方法可以研究流体流动的行为，而无需求解纳维-斯托克斯方程。格子玻尔兹曼方法 （LBM）就是这些方法中的一个。

如果使用纳维-斯托克斯方程，我们面对的将是一个复杂的偏微分方程组（PDE）。为了在数值上求解，我们必须应用各种技巧来离散化导数。一旦离散化完成，得到的将是一个庞大的非线性代数方程组有待求解。好累！而使用 LBM 方法，将完全绕过传统方法。在 LBM 中不需要求解方程组。此外，许多运算（我稍后将介绍）完全是本地运算。这使得 LBM 成为高度并行的方法。

我们可以在一个非常简单的框架中，将LBM视为一种"自下而上"的方法。在这种方法中，模拟在微观或"格子"域中进行。假设您有一个物理域或宏观域。我们要放大这个宏观域中的单个点，将有一些粒子根据粒子之间相互作用的"规则"而相互作用：

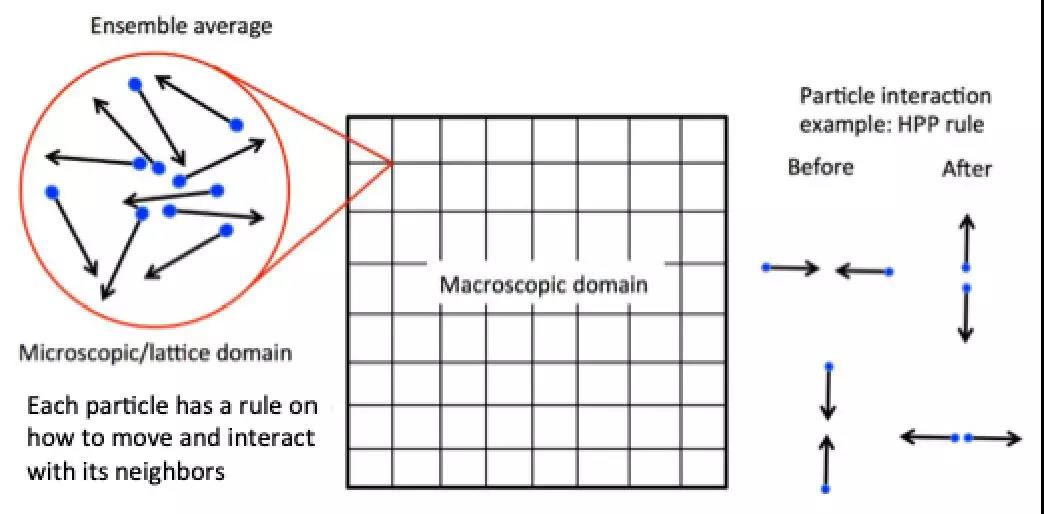
例如，如果两个粒子相互撞击，它们如何反弹？这些粒子遵循某种离散规则。现在，如果我们根据这些规则让粒子随时间演变（可以看到这与元胞自动机密切相关），并获取平均值，那么这些平均值可以用来描述某些宏观量。例如，我们在上图中看到的 HPP 模型（以哈代、波莫和德帕齐斯命名）可用于模拟气体扩散。

尽管这种离散方法听起来不错（20世纪70年代中期的研究人员确实尝试了其可行性），但它有许多缺点。其中一个主要问题是最终结果中有统计噪声。正是由于这些原则问题和试图解决这些问题的努力，LBM方法出现了。关于该方法的理论方面，网上有很多推导至最终方程的链接。在本文中，我想关注的是玻尔兹曼模拟的最终基础机制，而不是理论方面。因此，我仅谈一下开发风洞所需的最后方程。首先，假设密度和速度由以下方程描述：

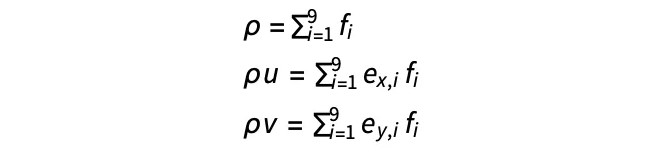
……其中 fi 为分布函数，ex, i 和 ey, i 为离散速度，且具有下列值：

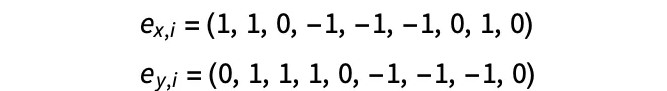
密度和速度的计算可以如下所示：

ex = {1, 1, 0, -1, -1, -1, 0, 1, 0};
ey = {0, 1, 1, 1, 0, -1, -1, -1, 0};
LBMDensityAndVelocity[f_] := Block[{rho, u, v},
rho = Total[f, {2}];
u = (f.ex)/rho;
v = (f.ey)/rho;
{rho, u, v}
];

这九个离散速度与其各自的分布函数 fi 相关联，可以形象地用下图表示：

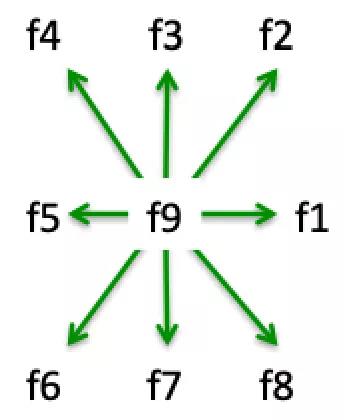
在格子域中的每个（离散）点上，将存在九个分布函数。使用这九个离散速度和函数 fi的模型称为 D2Q9 模型。如果分布函数 fi 已知，则速度场已知。由于速度场随空间和时间演化，我们认为这些分布函数也会随空间和时间演化。控制 fi 的时空演化方程由下式给出：

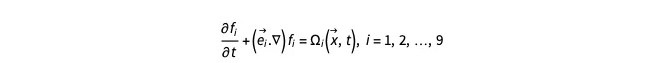
这里的 Ωi 是一个复杂的"碰撞"项，它基本上决定了各种 fi 如何相互交互。经过各种简化和近似，此方程可以化简为下式：

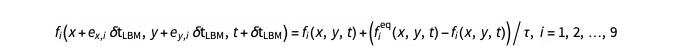
……其中 fieq 称为平衡分布函数，τ 称为松弛参数，δtLBM = 1 是格子玻尔兹曼域中的时间步长。该近似称为 BGK 近似，生成的模型称为格子 BGK 模型。关于这两个项的详细定义将在稍后介绍。这些函数的空间和时间演化分两个步骤完成：（a） 迁移步骤；和 （b） 碰撞步骤。

由于δtLBM = 1 且

均为1或者0，迁移步骤由下式给出：

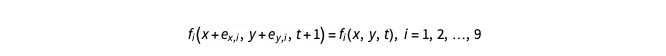
要将迁移步骤可视化，想象一下离散化的域。此域的每个网格点上有 9 个分布函数（如下图所示）。请注意每个网格点的各种颜色。每个箭头的长度指示相应的分布函数的大小：

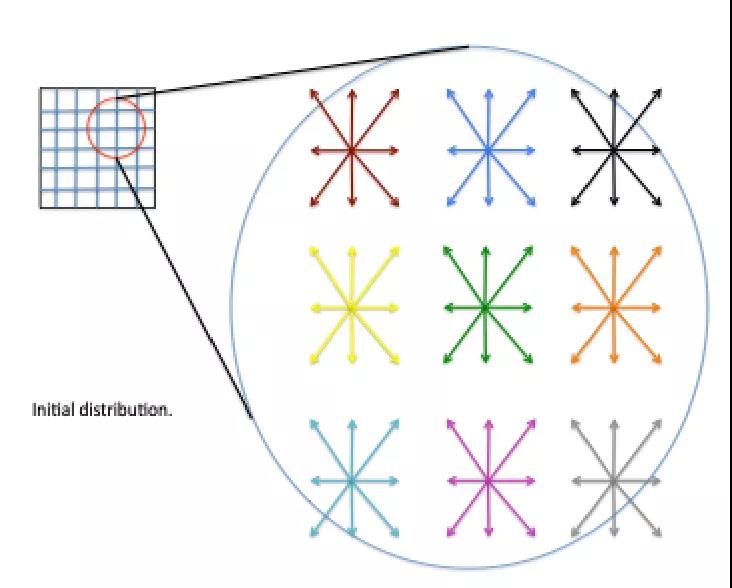
要将迁移步骤可视化，想象一下离散化的域。此域的每个网格点上有 9 个分布函数（如下图所示）。请注意每个网格点的各种颜色。每个箭头的长度指示相应的分布函数的大小：

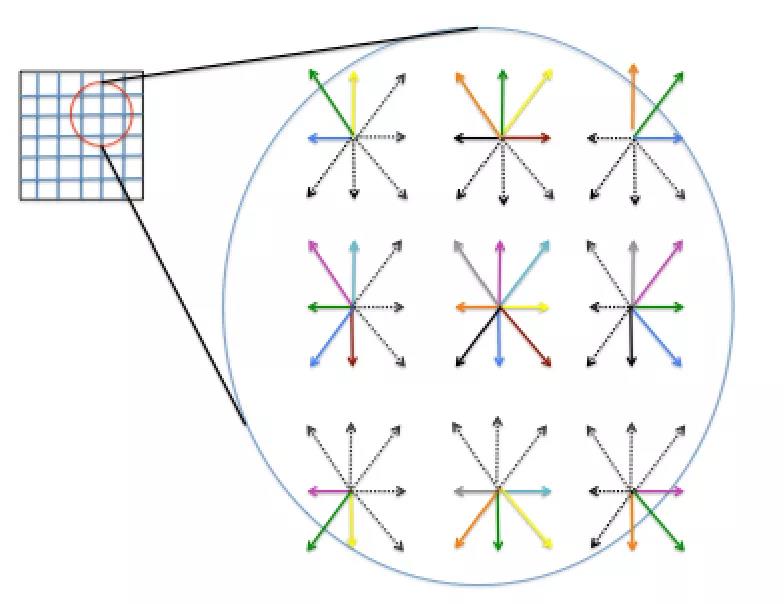
注意颜色和它们结束的位置。将注意力集中在中心点会有帮助。在迁移步骤之前，箭头（表示不同的fi）都是绿色的。在迁移步骤之后，请注意绿色箭头落在周围网格点的位置。简言之，这就是迁移步骤。在 Mathematica 中，此步骤使用内置函数RotateLeft或 RotateRight 可以非常容易地完成。这里我们使用 RotateRight：

当进行迁移时，必须特别注意解决风洞的边界问题。在迁移完成后，域的边角处某些 fi会变得未知。原理图（如下图所示）显示哪些 fi 对于其各自的边和角未知。未知数由虚线箭头表示：

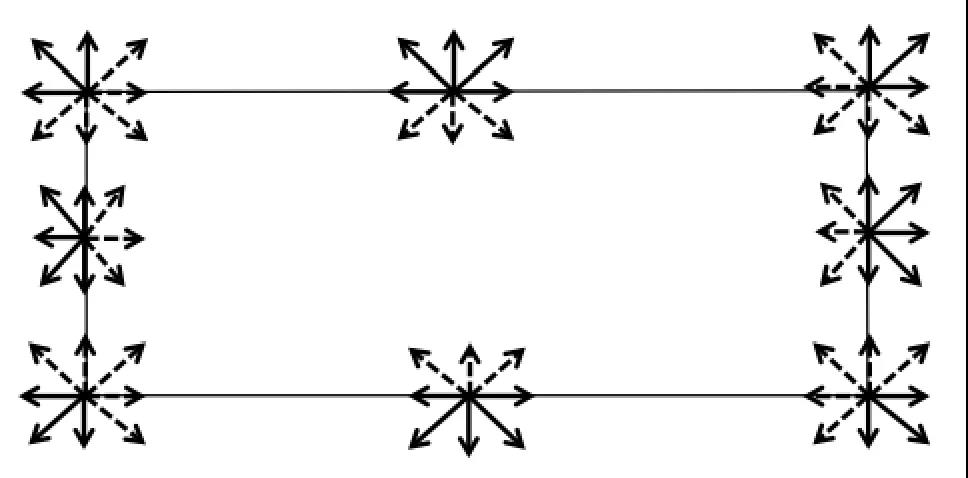
为了理解未知的 fi 如何计算，让我们考虑一下风洞的顶壁。对于此边，f6, f7, f8是未知的。我们令 ：

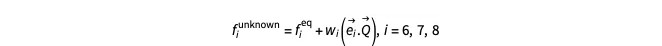
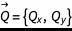是二维未知向量，而 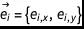和 fieq 是平衡分布函数，定义为：

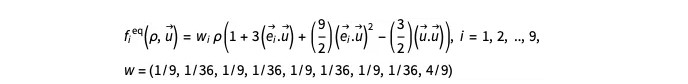
Ho, Chang, Lin 和 Lin在他们的论文中详细介绍了这种方法。此运算（实际上是一个高度可并行的运算）可以在 Mathematica 中有效地完成 ：

请注意，fieq 完全由速度和密度决定。将其代入速度和密度方程式，我们得到：

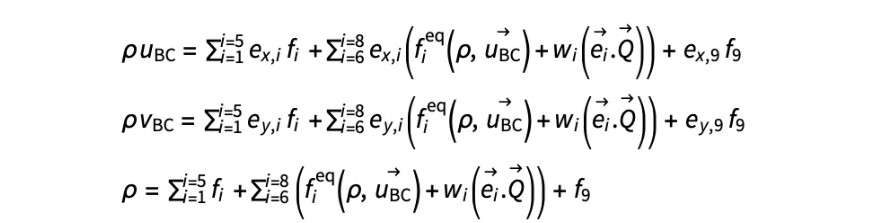
...其中 UBC, VBC 是用户为边界指定的速度。生成的这些方程是线性的。有三个未知数 {ρ, Qx, Qy}，并且有三个等式，可以很容易地使用 LinearSolve 或 Solve 求解。同样的步骤适用于所有边和角。由于这是一个小的3 × 3系统，我们可以符号式地预先计算缺失分布的表达式。因此，对于顶壁，我们将有：

一旦 {ρ, Qx, Qy} 已知，将这些值代入即可获取未知数：

在处理溢出边界条件时，我们实际上是试图跨边界施加 0-梯度条件，即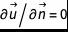
。最简单的一件事就是使用后面一个网格的速度，并用它来计算边界上的fi。然而这将导致不准确的结果，并且在很多情况下，这些结果也将不稳定。

考虑右壁，如下图所示：

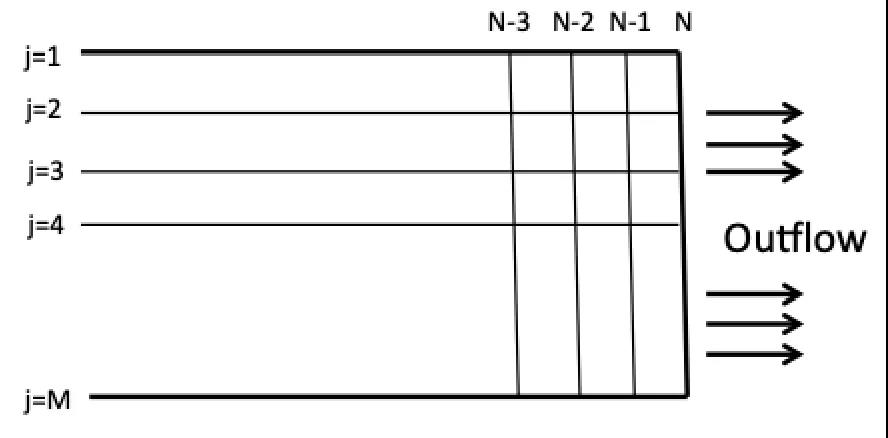
迁移步骤之后，分布 f4, f5, f6 未知。为了对分布函数 fi 施加溢出条件，我们使用以下关系：

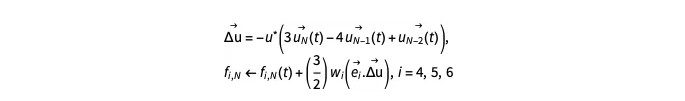
…… 其中

uk(t)

是上一个时间步在网格点(j, k), j = 1, 2, … 的速度，M 和 fi,N(t) 是上一个时间步长的分布。标量项u*必须为正数。一个好的候选是边界处的正常速度，所以对于左右壁，有

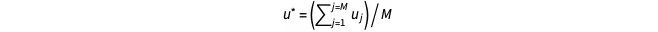
，对于上下壁，

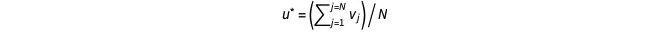
。如果u*是0，它可以被特征格子速度所取代。请注意，未知分布会根据哪面壁具有溢出条件而变化。例如，如果它是顶壁，则f6, f7, f8未知。Yang的文章（https://www.sciencedirect.com/science/article/pii/S0898122112006736）详细介绍了这种溢出处理方法。

而第二种方法只需做以下操作：

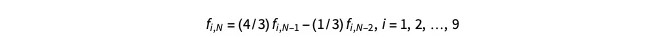
此方法比第一种方法简单得多，并且基于对每个分布函数应用二阶逆向差分公式。

一旦迁移完成并施加边界条件后，将进行"碰撞"（回忆一下基于规则的方法）。此步骤基本上是找出整体平均粒子将如何相互交互。此步骤有点复杂，但使用 BKG 近似，碰撞步骤可以写作：

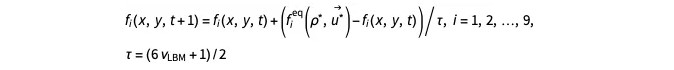
……其中是迁移步骤和边界调整步骤后计算的密度和速度。vLBM 是格子玻尔兹曼域中的运动粘度，τ 是松弛参数。这个项非常重要，这里详细介绍一下。

这在 Mathematica 中是两行非常简单的代码：

从视觉角度来看，碰撞后分布函数根据前面的公式进行调整，我们得到了新的分布：

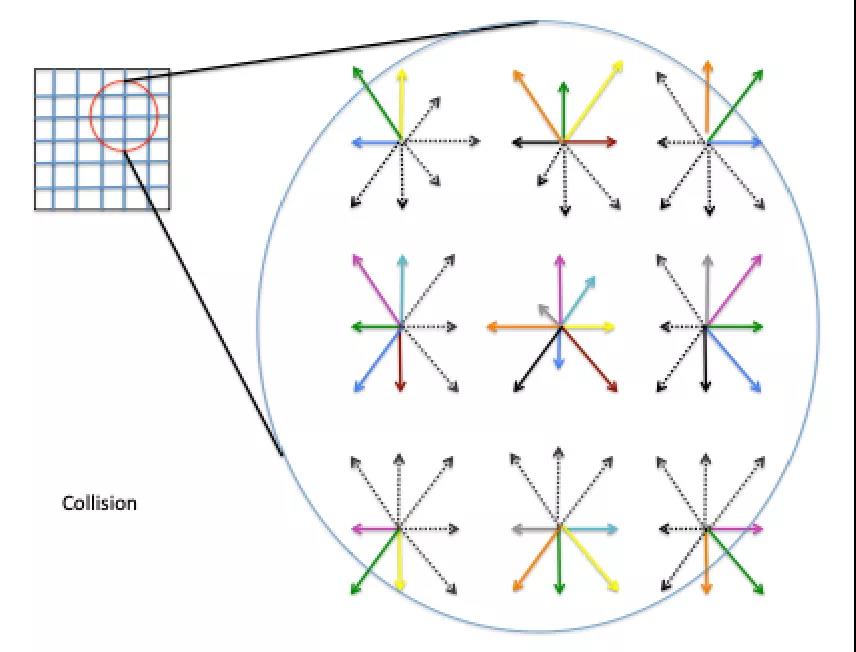
请注意箭头长度的变化。就是这个！这就是运行格子玻尔兹曼模拟所需要的一切。

使用雷诺数将模拟变为现实

那么，如何模拟传说中的纳维-斯托克斯方程？为了回答这个问题，我们必须进行大量的数学和多尺度分析，但简而言之，feq的形式决定了LBM模拟的宏观方程。因此，使用适当的平衡函数可以模拟一大堆偏微分方程。读者有兴趣的话，可以去网上找到很多人们使用LBM方法进行模拟的精彩范例。

我们已经了解了LBM的基本机制，下一个显而易见的问题是：在基于格子的系统中执行的模拟如何转换到物理世界中来？这是通过匹配格子系统和物理系统的非维参数来完成的. 在我们的例子中， 非维度参数只有一个 ：雷诺数。雷诺数 （Rey） 的定义如下：

…其中Uphy是一个特征速度，Lphy是特征长度，vphy是物理域中的运动粘度。为了模拟流体，用户需要指定雷诺数、特征速度和特征长度。这三条信息确定了运动粘度，随后确定了松弛参数τ。使用这些信息和与 LBM 关联的基础方程，计算模拟的内部参数。

特征格子速度 ULBM 不能超过（此数字计算为格子域中的声速）。格子速度必须明显低于此值，才能正确模拟不压缩性。通常，格子速度为ULBM= 0.1。同样，特征格子长度LLBM表示格子域中用于表示物理域中特征长度的点数。LLBM将是一个整数，并且通常由用户定义。

让我们通过一个例子看一下如何将格子模拟与物理模拟联系起来。让我们假设 Rey = 100，Uphy = 1，Lphy = 1，风洞的物理尺寸为Lw = 15Lphy，Hw = 5Lphy. 对于格子域，我们假设 ULBM = 0.1，LLBM = 10。格子风洞尺寸为LW,LBM = 15 × 10 = 150，Hw,LBM = 50。格子域中的粘度为：

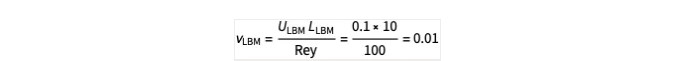
这意味着 BGK 模型中的松弛参数τ为：

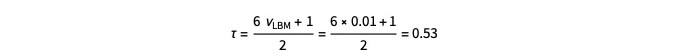
现在，我们拥有运行模拟所需的所有数量。如果我们现在让模拟中的每个晶格时间步长为δtLBM = 1，那么我们需要知道δtphy是什么。这是通过等同粘度来完成，并且通过以下条件给出：

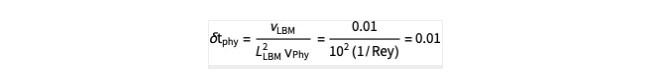
因此，如果我们想要运行的模拟 t = 100（时间单位），那么在晶格域中，我们将迭代 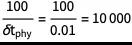步。

雷诺数是一个显著的非维参数。雷诺数不是指定我们模拟的流体及其速度和维度，而是将它们联系在一起。也就是说，对于长度、速度和流体介质截然不同的两个系统，只要雷诺数保持一致，这两个流体将具有相同的性能。

向风洞中添加物体

现在我们来讨论下如何将物体放到风洞中。一种方法是将原始物体离散化成锯齿状，并将其与网格对齐，然后在每个步长的边和角上施加无滑动边界条件：

这种方法并不理想，因为它扭曲了原始物体。如要更好的表示物体，需要使用极其精细的网格，但这让计算成本昂贵并且造成不必要的浪费。另外，尖锐的边角会使流体产生不希望的行为。第二种方法是将物体浸入到网格中。物体的边界被离散化，并浸入至域中：

对具体物体的边界进行离散，可以使用内置函数BoundaryDiscretizeRegion 轻松实现。我们可以指定 Disk 或 Circle 来生成一组点表示圆形物体的离散化版本：

这种将物体离散并放入网格的方法称为浸入边界法（IBM）。一旦离散化的物体被浸入，就需要模拟该物体对流体的影响，以确定其遵循边界速度条件。一种使流体"感受"到浸入物体存在的方法是称为直接施力方法。这种方法通过对演化方程添加施力项Fi，对格子BGK模型进行了修正：

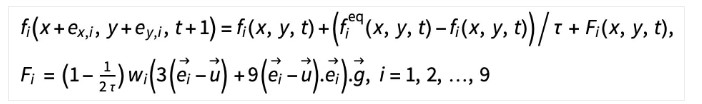
……其中 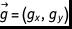为物体边界在网格点上产生的矫正力。计算速度的公式现在修正为：

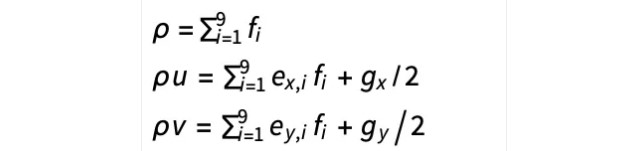
修正力的计算公式为：

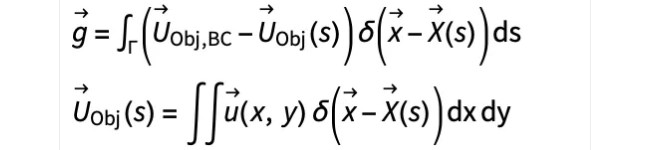
……其中 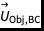是物体的边界条件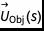，是不存在物体的情况下在物体边界处的速度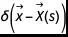，是增量函数的近似值， 是物体边界点的位置，通常称为拉格朗日边界点。有几种选择可以使用。我们将使用以下紧凑支持的功能：

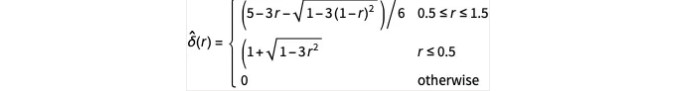
这种近似也称为柔化函数内核，可以使用分段函数进行定义：

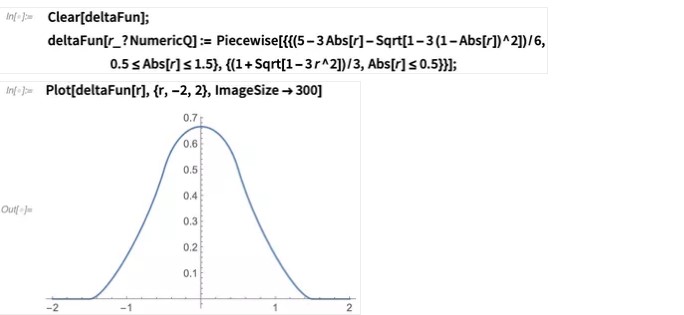
由此得到二维函数 δ(x – X, y – Y)：

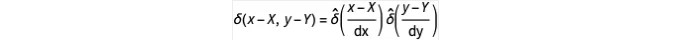
...其中dx，dy是缩放参数。对于拉格朗日点(Xi, Yi)，指定了δ函数。下面是以（1/2，1/2）为中心并按1缩放的δ函数的外观 ：

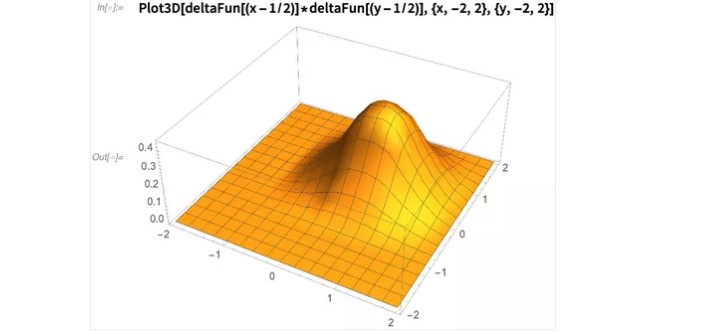
让我们通过一个示例来说明这个沉浸式边界的概念，以及如何构造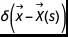函数并将其用于逼近函数。假设一个圆浸入矩形域中：

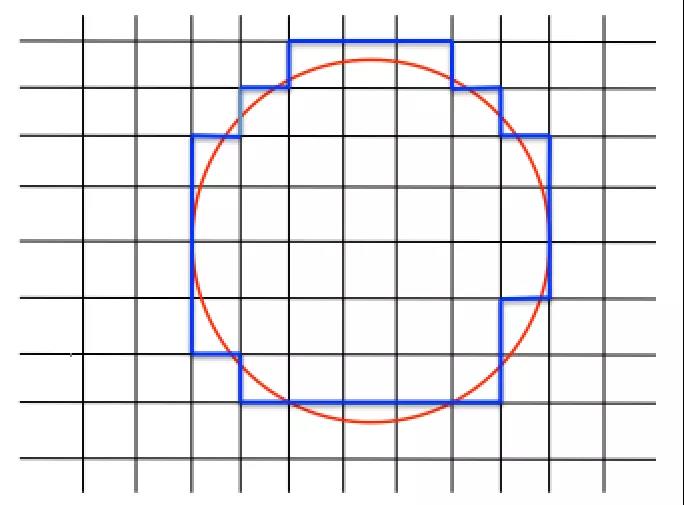
每个拉格朗日边界点（蓝色）都会影响一定半径内的网格点（垂直线和水平线的各个交点），如下图所示：

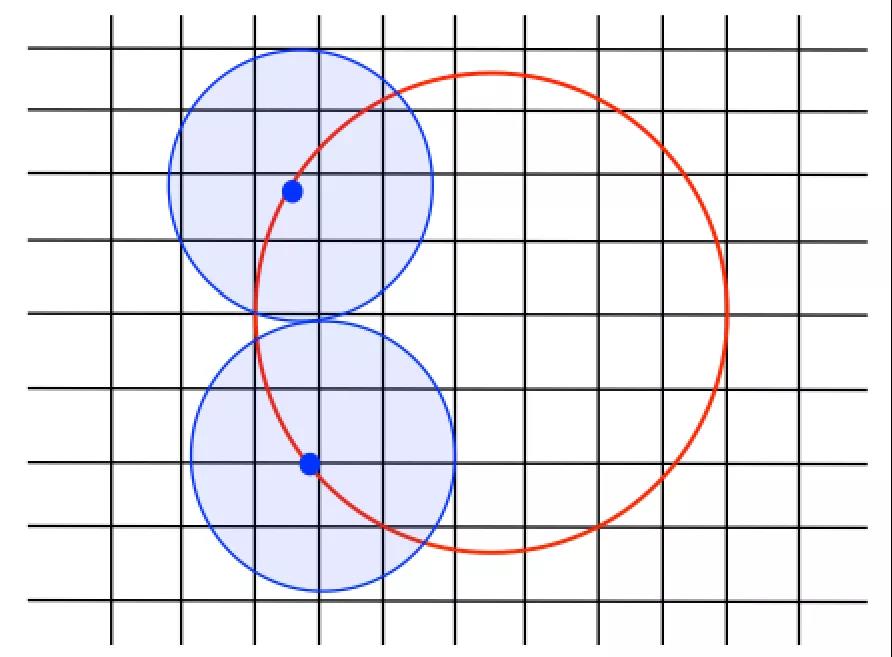
为了获得受每个拉格朗日点影响的网格点，我们使用了Nearest函数：

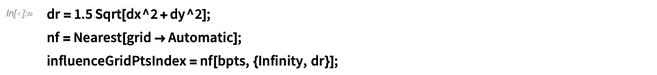
离散点的函数δ(x – X(s), y – Y(s))实际上成了一个矩阵：

该矩阵现在可以用于计算拉格朗日点的值。例如，让我们假设底层网格上具有由h(x, y) = Sin(x + y)定义的值，则拉格朗日点的值计算如下：

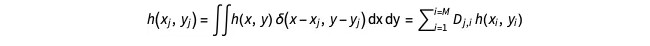
...其中D是δ的离散化，h(xj, yj)是在(xj, yj)处要计算的函数值：

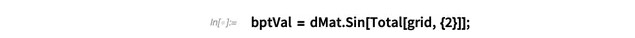
我们可以将计算出的插值与实际值进行比较：

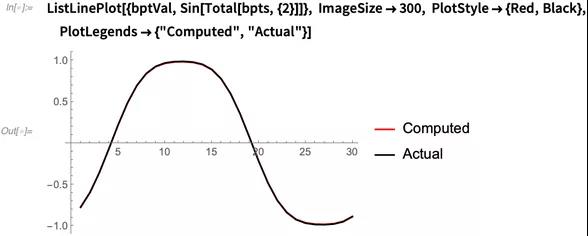
同样，可以使用拉格朗日点上的函数值来计算网格上的函数值：

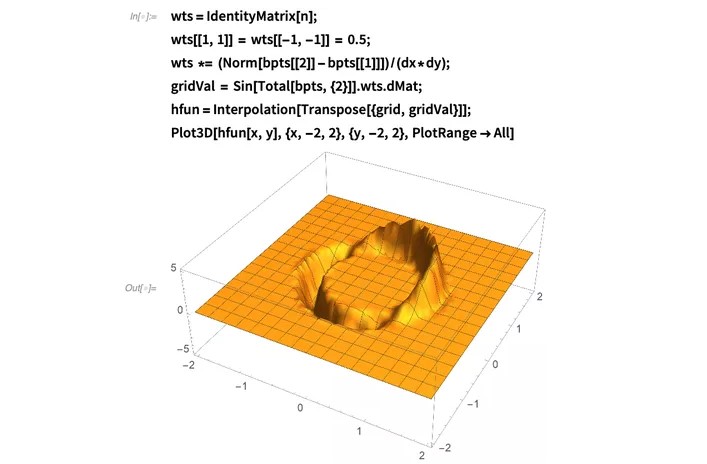
如您所见，由于δ函数具有紧支集，因此只有位于其影响半径内的网格点才会获得插值。所有不在支撑半径内的网格点均为0。

因此，在这里提醒读者，格子玻尔兹曼模拟中的一个步骤包括以下步骤：
1、执行迁移步骤。
2、在边界处调整分布函数。
3、执行碰撞步骤。
4、计算速度。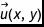
5、计算物体在拉格朗日边界点的速度。
6、对于物体的每个边界点，计算在该点施加边界条件所需的校正力。
7、使用在步骤6中获得的力计算点阵网格点处的校正力。
8、执行迁移和碰撞步骤，考虑到作用力。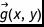
9、计算密度和速度。

到此，我们对使用二维LBM运行风洞模拟所需的所有要素已经介绍完毕。

示例

为了使此风洞易于使用，所有函数都放入了名为 WindTunnel2DLBM 的程序包(https://blog.wolfram.com/data/uploads/2019/10/WindTunnel2DLBM.zip) 中。它包含许多功能，并且用户可以轻松对问题进行设置。建议有兴趣的用户仔细阅读程序包文档，以了解详细信息。这里将重点介绍各种示例并展示我们的计算型风洞设置的灵活性。

第一个示例是风洞中的流体。这也许是最简单的情况。域及其相关边界条件的示意图如下所示：

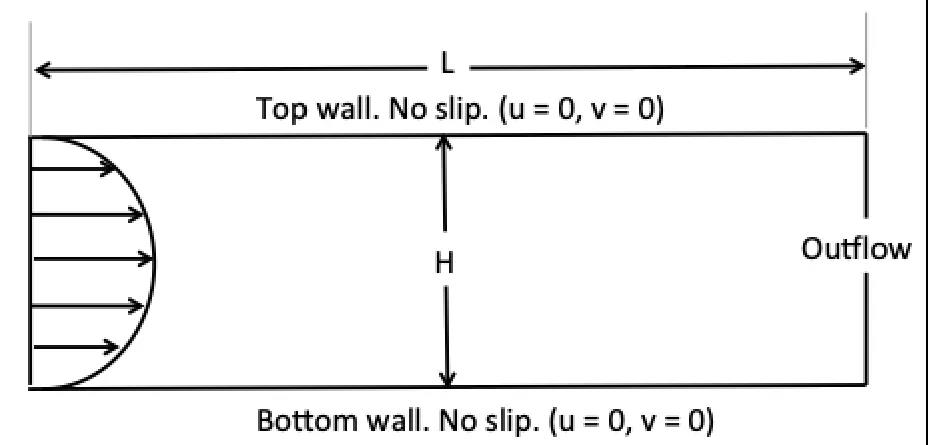
在这种情况下，该问题只有一个长度尺度：风洞的高度。因此，这成为我们的特征长度尺度。在这种情况下，特征速度是来自进口的最大速度，该速度设置为1。剩下的就是指定要执行模拟的雷诺数。这也是由用户定义。让我们将风洞的长度设为6个单位，从（0,6），将高度设为2个单位，从（-1,1）。现在，我们设置模拟：

请注意，我们在此处未提供任何边界条件信息。这是因为风洞默认气流在通道情况下，因此自动施加所有边界条件。我们只需要指定特征信息和风洞的尺寸即可。

使用固定的时间步长执行模拟。时间步长在内部计算，可以从以下属性访问：

现在让我们以5个时间单位运行模拟：

我们可以在模拟的最后一步查询数据：

解决方案可以通过多种方式可视化。对于2D模拟，流线图可以显示一些有用的信息，让我们可视化流线图：

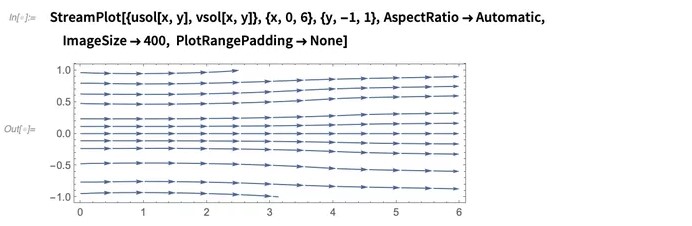
请注意，流线并非完全平行（存在一些偏差）。要了解原因，让我们看一下x各个位置处速度场的u分量的分布：

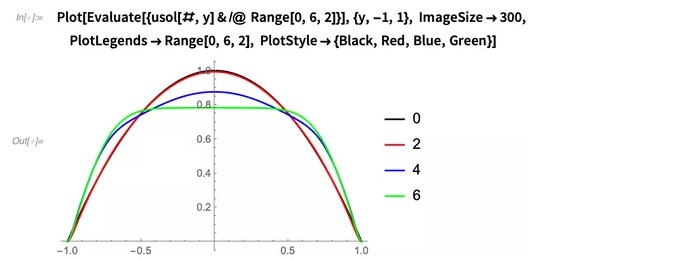
这表明速度具有空间依赖性。对于此特定问题，我们应该期望流量达到稳定状态，即流量不应随时间变化。让我们以另外20个时间单位运行模拟，并查看速度曲线：

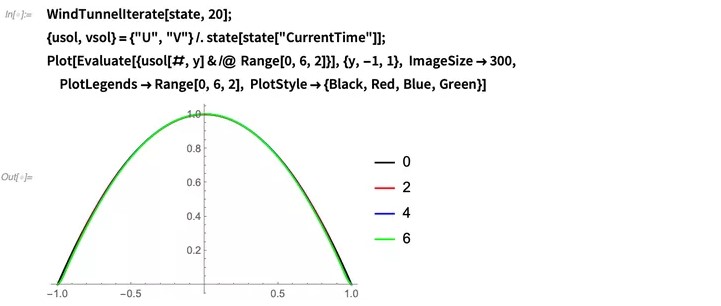
我们看到在各个x位置的速度分布几乎彼此相同。这表明流确实达到了稳定状态。

箱内流体问题

现在，让我们看一下经典的"箱内流体"问题。这是域的示意图和边界条件信息：

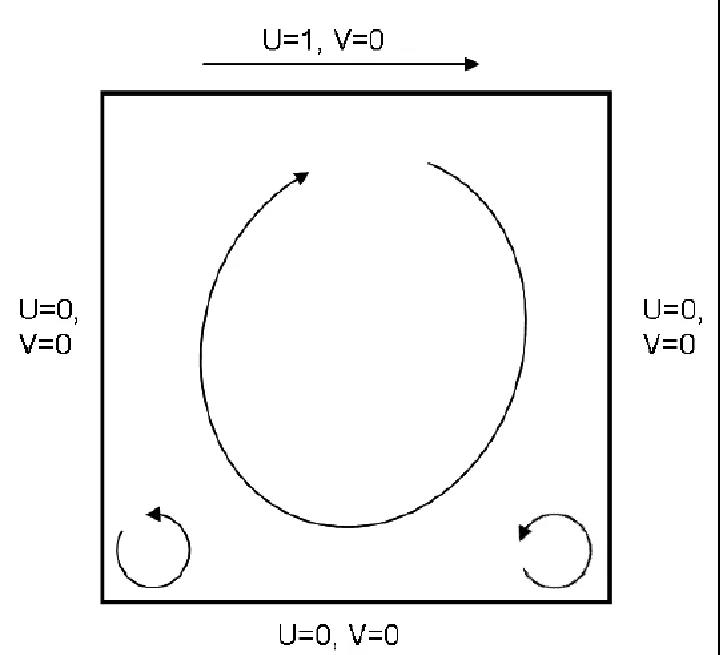
顶壁以水平速度1（长度单位/时间单位）移动，而其他所有壁都是固定防滑壁。箱内的圆圈表示可能发生的流体行为。当顶壁移动时，壁会拖动下方流体，从而导致流体旋转-这是原理图中的大圆圈，它代表了涡旋。如果主旋涡有足够的强度，则可能引发较小的次级旋涡。我们假设涡旋强度与雷诺数有关。让我们看看以雷诺数100运行模拟会发生什么：

现在，我们迭代50个时间单位：

可视化结果表明，在中间附近形成了一个主旋涡，而箱的右下方形成了一个较小的次级涡旋：

如果雷诺数增加，则次级涡流会变得更强，并且额外的涡流会在拐角开始形成。让我们看一下雷诺数为1,000的情况：

我们再次迭代50个时间单位：

可视化结果：

注意，主旋涡已移近中心。从它的外观来看，已经足够强大到在域的左下角和右下角形成次级涡旋。

现在让我们看看如果在"高"箱而不是正方形箱上进行仿真会发生什么。边界条件保持不变，但域沿y方向变化：

运行模拟并使用 ProgressIndicator 跟踪进度。此模拟将花费几分钟：

可视化流线：

在高箱场景中，在顶壁附近形成了一个主旋涡，而该旋涡又在其下方创建了另一个旋涡。如果第二个涡旋强度足够大，它将在箱的底角产生涡旋。

我们已经看到风洞为我们提供的灵活性。现在让我们在风洞中放置一个物体并观察气流的行为。对于此示例，使用圆形物体：

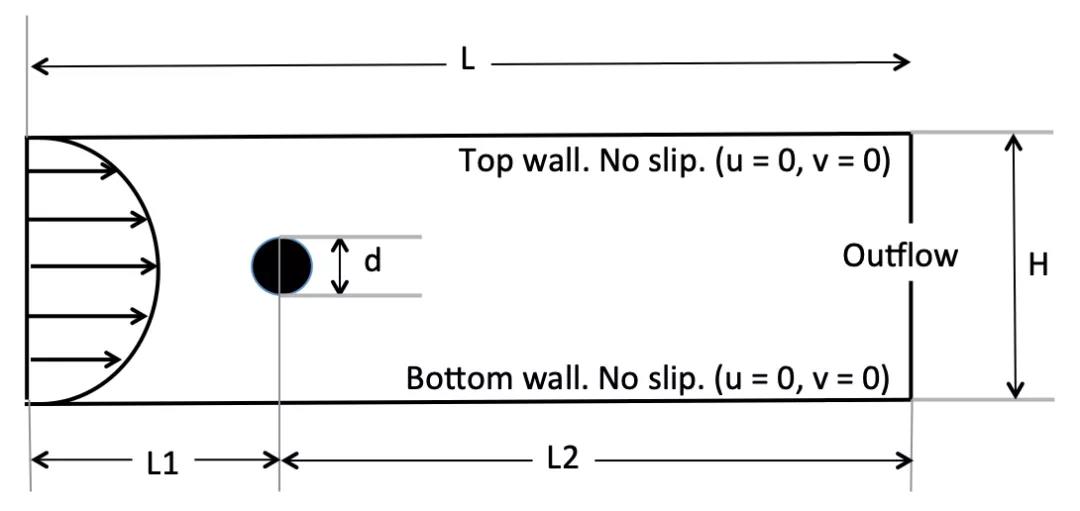
这与通道中的流体相同（我们的第一个示例），但物体是放置在通道中。注意，现在存在两个长度尺度d和H。特征长度的选择尽管是任意的，但必须与流体的物理特性相联系。在此示例中，如果要增大或减小物体的大小，则可以预期其后面的流型将发生变化。因此，自然的选择是使用d作为特征长度。

让我们将圆柱体放置在域的（3,0）处。令圆柱体的大小为1个长度单位。也就是特征尺度将为1。设域大小为 (0, 15) × (–2, 2)。该物体用 ParametricRegion指定：

在开始模拟之前可视化隧道是一个好主意，以确保物体位于正确的位置：

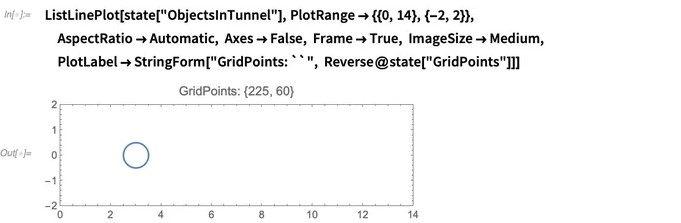
让我们模拟10个时间单位的流体：

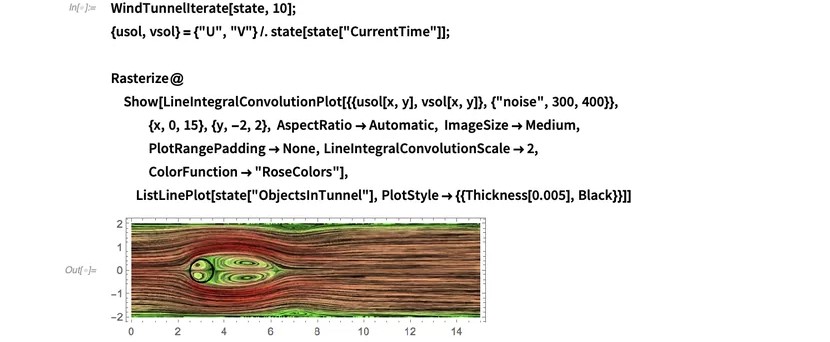
这里有两点要注意：圆柱体后面的对称涡流对和圆柱体内的流体。一个特写镜头表明，圆柱内也有一些流型：

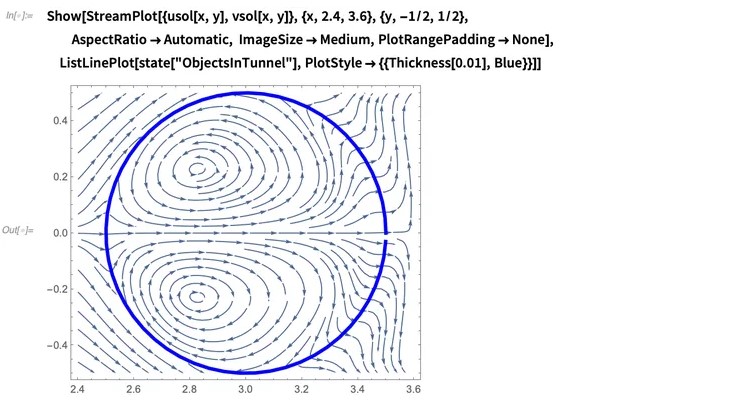
这种行为的发生是因为我们正在使用IBM。如前所述，IBM计算一组要施加到网格点上的力，以使表示该表面的表面速度为0。它不指定圆柱体内应该发生什么。因此，作为不可压缩的流体，在圆柱体内也存在流型。重要的是，物体边界处的速度为0（无滑动）。

现在让我们继续迭代30个时间单位，看看圆柱体后面的流型发生了什么。有时，查看另一个称为涡量（vorticity）的变量可能会帮助我们更好地了解正在发生的事情：

设置等值线的配色方案：

可视化涡量：

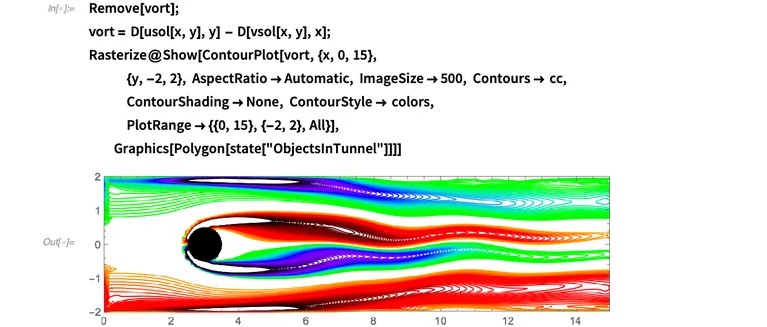
现在，我们注意到对称性已被破坏，并被"波浪"行为所取代。旋涡清楚地表明了波浪状的行为。我们在这里看到的被称为圆柱体带来的不稳定性。这种不稳定性继续扩大，最终在圆柱体后方开始形成涡流。这种现象称为"涡旋脱落"。在圆柱体表面产生了一个剪切层，该剪切层被带到下游。

该涡旋脱落还取决于雷诺数。如果数值足够小，则不会有任何脱落。但是，如果雷诺数达到100 - 150左右，则会观察到脱落。为了正确地观察这种现象，最好能看到这种流动的时间演变。第一步，通过定特征项和义隧道中的物体来设置问题：

为了产生涡量的时间演变，我们将在每个时间单位提取解并生成一系列图形：

运行模拟可以清楚地看到，在圆柱体的背面形成了两个涡流，剪切层缓慢地受到扰动，然后振幅逐渐增大，最终分裂成涡流脱落：

观察移动物体引起的扰动

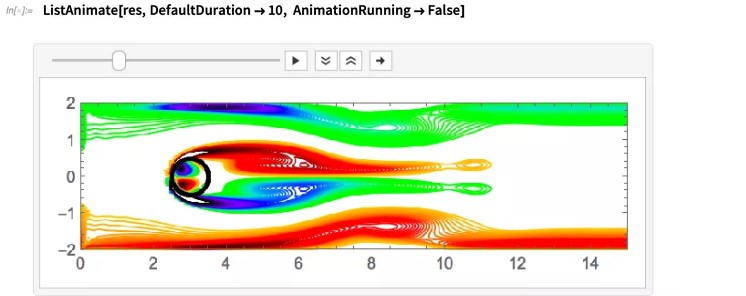
在下一个示例中，我们将采用沉浸边界处理法，将一个圆形储罐"浸入"风洞内部。储罐边界处的速度为0。在此储罐内，我们将浸入一个椭圆形物体。该物体放置在储罐壁附近，并在储罐边界遵循圆形路径。格子玻尔兹曼法对于浸没边界的的灵活性使我们对移动物体有极大的灵活性。目的是研究当该物体移动通过静止流体时会产生什么样的扰动。

通过定义特征项来设置问题。在这种情况下，将以雷诺数400进行仿真。特征长度和速度为1。隧道中有两个物体。第一个是固定的大型圆形储罐。第二个是将在此储罐内移动的椭圆形物体：

检查潜在问题的几何形状永远是一个好主意。我们可以通过在初始化时简单地提取离散化对象来实现。我们可以看到一切各归其位：

和刚才一样，我们将研究流体的涡量等值线。让我们首先定义配色方案和将要绘制的等值线的水平：

现在模拟以60个时间单位运行：

运行流体扰动的时间演变表明，在达到更均匀的圆形扰动之前，最初在储罐内形成了非常漂亮的几何图案：

在弯曲和有障碍物的管道中的流体

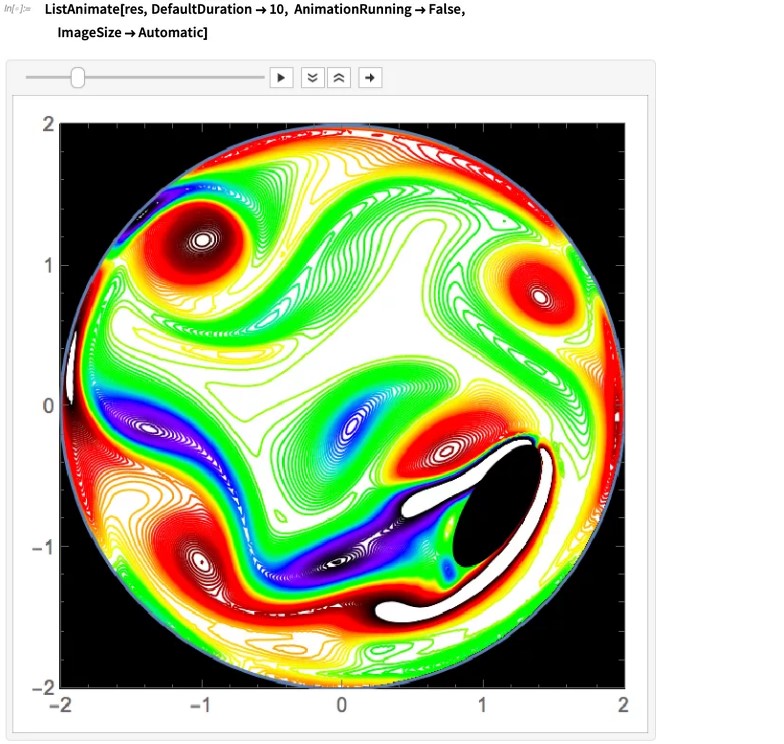
出于好奇（和好玩），在下面的几何体中会有怎样的流型？

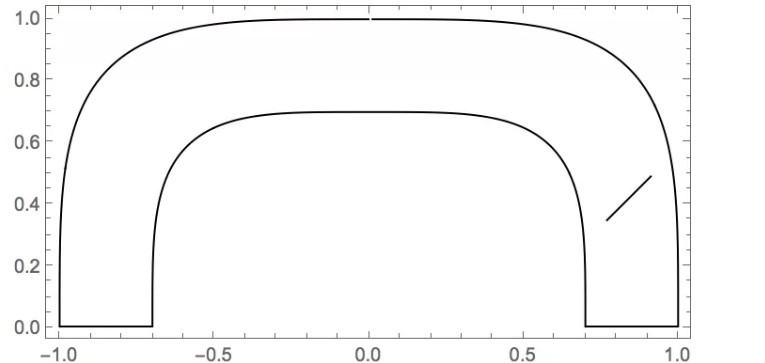
流体从右端进入管道，然后向上移动，然后从左端排出。塞子在右端的作用是什么？它会如何影响排水？

使用我们当前的设置，问题非常容易弄清楚。同样，我们只是将管道和其中的障碍物浸入风洞中。风洞的左边界、右边界和顶边界被指定为零速度。底部边界的流出条件为-1 <= x <=-0.7，0速度条件为-0.7 <= x <= 0.7，抛物线速度曲线为0.7 <= x <= 1：

运行40个时间单位：

让我们绘制涡量：

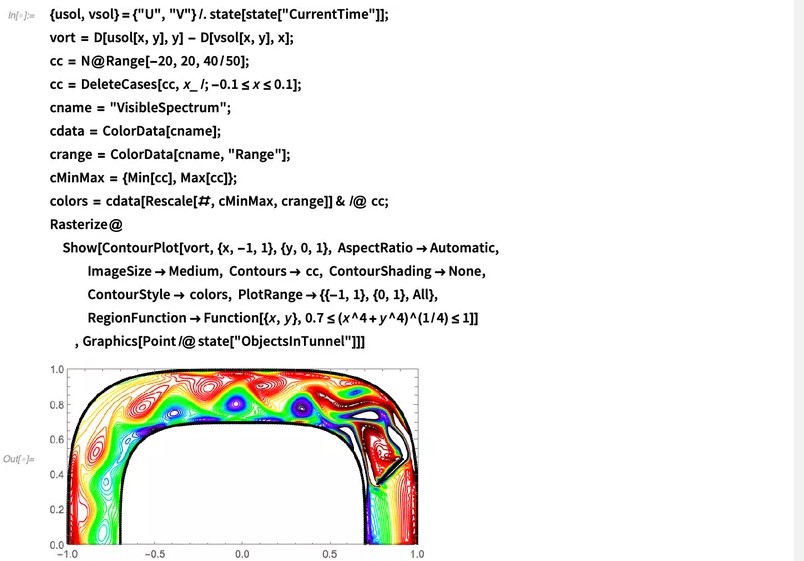
我们看到障碍物/塞子会产生涡流脱落，并沿着管道向下移动。让我们看一下y = 0处的速度：

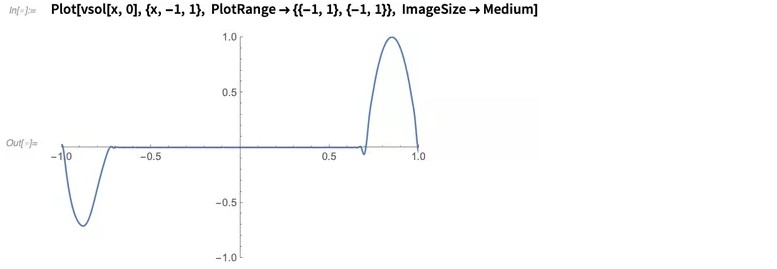
如果比较出口（左侧）和入口（右侧）之间的速度曲线，会看到出口速度几乎是入口速度的一半。这足以表明，塞子使管道左端排出的液体减少，这和我们的预期一样。

模拟翼型上的流体

作为最后一个例子，让我们看一下机翼周围的流体。翼型或称翼剖面，是使得飞机升空的基本要素。机翼的类型很多，但我们将重点介绍一种简单的机翼，由参数方程 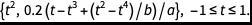表示。参数a控制翼型的厚度，参数b控制翼型的曲率：

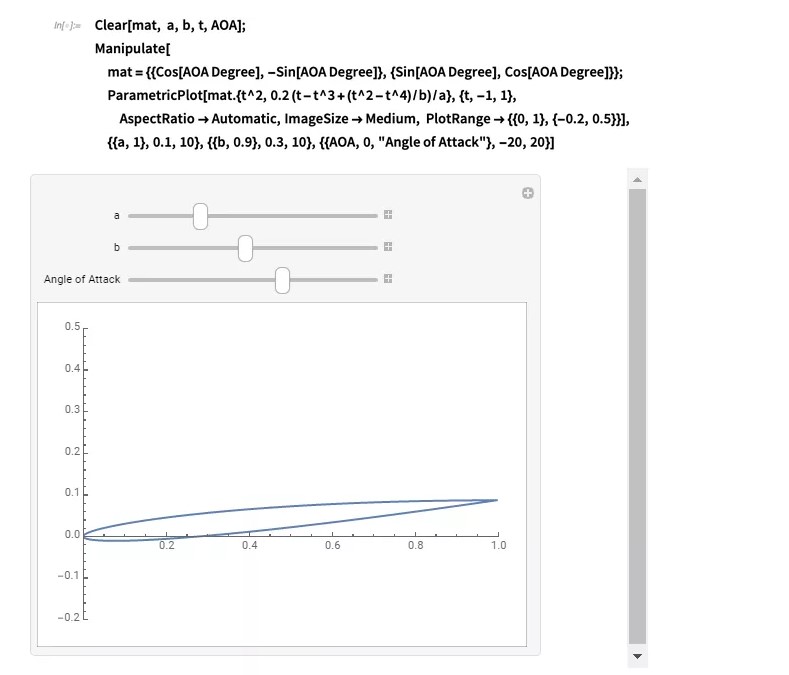
为了使飞机"升空"，即离开地面，机翼顶面的压力分布应低于底面的压力分布。这种压力差会导致机翼（以及与其相连的所有物体）向上抬升。通过让风以相当高的速度吹过其表面来实现该压力差。第二个考虑因素是机翼通常需要倾斜以具有"攻角"。这样做可以确保更大的提升。我们还将给机翼一个-10\[Degree]的攻角。该模拟将在雷诺数为1,000的情况下运行。现在要指出的是，雷诺数为1000是一个很小的值。小型飞机的典型雷诺数约为100万。由于网格尺寸较大，无法在笔记本电脑上进行全尺度模拟。但是，即使雷诺数只有1,000，我们也能够很好地理解其潜在的动力学原理。在这个例子里，均匀的流体填充从左侧进入。顶部和底部隧道边界设置为周期性，右侧边界设置为流出。此处的特征长度将是机翼的厚度：

在开始模拟之前，提取离散化的对象，并检查其是否位于风洞内的适当位置：

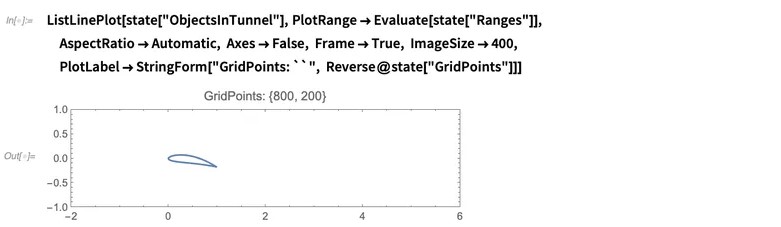
注意到有大量的网格点。这是因为我们允许20个晶格点来解决薄机翼的问题。现在，我们以10个时间单位运行模拟，这需要一点时间才能完成，原因是：（a）分辨率（即运行此模拟所需的网格点数）非常大 (800×200)；（b）要完成模拟，必须执行20,000次迭代：

开始迭代过程：

让我们首先看一下涡量图：

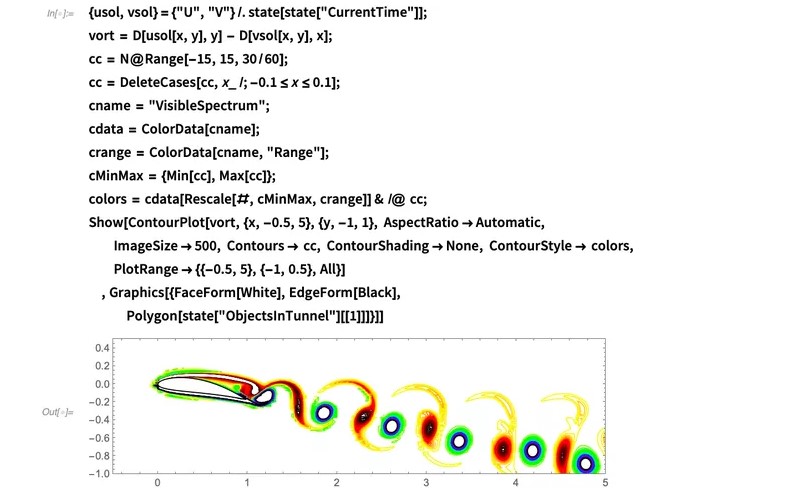
就像钝体的情形一样，我们看到了涡旋脱落。对于机翼而言，这实际上不是理想的属性。理想情况下，我们希望流体能够拥抱表面。当气流分开时（如您在机翼的顶面所看到的），压降无法正确实现，并且机翼将无法产生升力。

现在让我们看看压力。除了绘制压力外，我们还将绘制一个无量纲的参数，称为压力系数，由 Cp = 2(p – p∞)/(ρLBM U2LBM) 定义，其中 p∞ 是远上游的压力。我们对物体表面的压力感兴趣：

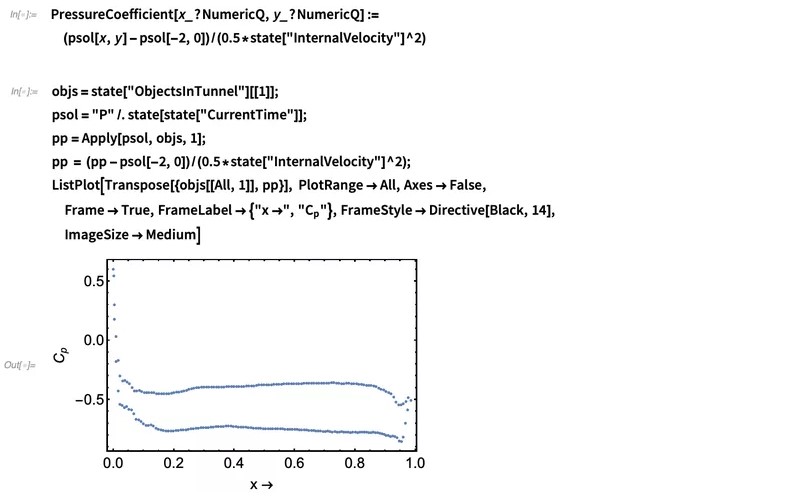
您会注意到这里有两条直线。下方的直线代表顶面上的压力，而上方的线代表底面上的压力。显然，尽管与翼型有所分离，但我们仍会获得一些压力差。我们还可以绘制压力等值线，并在翼型附近对其可视化：

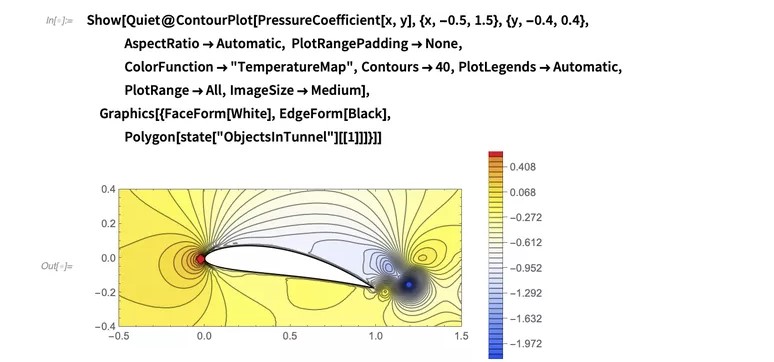
如果仔细查看配色方案，的确会发现顶面压力小于底面压力。因此，这种翼型也许有希望。我们刚刚探讨的流体动力学特性被称为伯努利原理，该原理已在航空（如我们在此处看到的）和汽车工程等领域得到应用。

这不过是开始，还有更多示例等你去亲自尝试！我们这里提供另辟蹊径，来用Mathematica 来研究并模拟流体动力学问题。LBM与IBM结合使用，对研究和分析流体流动是一个很好的工具。借助 Mathematica 的内置函数，实现数字风洞的组装非常简单。软件包 WindTunnel2DLBM 帮助我探索了流体动力学领域中许多引人入胜的概念（以及令人叹为观止的可视化）。我希望您也能从中得到启发，并深入研究流体流动现象。